题目内容
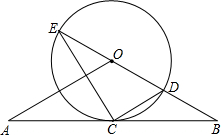
如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E、D，连接EC、CD．
（1）求证：直线AB是⊙O的切线；
（2）试猜想BC，BD，BE三者之间的等量关系，并加以证明．
（1）求证：直线AB是⊙O的切线；
（2）试猜想BC，BD，BE三者之间的等量关系，并加以证明．
（1）证明：如图，连接OC．
∵OA=OB，CA=CB，
∴OC⊥AB．
∴AB是⊙O的切线；
（2）BC2=BD•BE．
证明：∵ED是直径，
∴∠ECD=90°，
∴∠E+∠EDC=90°，
又∵∠BCD+∠OCD=90°，∠OCD=∠ODC，
∴∠BCD=∠E．
又∵∠CBD=∠EBC，
∴△BCD∽△BEC．
∴
=
，
∴BC2=BD•BE．
∵OA=OB，CA=CB，
∴OC⊥AB．
∴AB是⊙O的切线；
（2）BC2=BD•BE．
证明：∵ED是直径，
∴∠ECD=90°，
∴∠E+∠EDC=90°，
又∵∠BCD+∠OCD=90°，∠OCD=∠ODC，
∴∠BCD=∠E．
又∵∠CBD=∠EBC，
∴△BCD∽△BEC．
∴
| BC |
| BE |
| BD |
| BC |
∴BC2=BD•BE．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
写推理过程）写出五条结论即可．
