题目内容
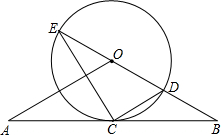
如图,已知点C在⊙O上,延长直径AB到点P,连接PC,∠COB=2∠PCB.
(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧上一动点,当M点运动到使△ABM的面积最大时,CM交AB于点N,求MN•MC的值.

(1)求证:PC是⊙O的切线;
(2)若AC=PC,且PB=3,M是⊙O下半圆弧上一动点,当M点运动到使△ABM的面积最大时,CM交AB于点N,求MN•MC的值.

(1)证明:连接BC,∵AB是直径,
∴∠ACB=90°.
∵∠COB=2∠PCB,∠BOC=2∠OAC,
∴∠CAB=∠BCP.
∴∠PCO=90°.
∴PC是⊙O的切线.
(2)由题意知,M为
的中点,
过M作⊙O的直径MD,连接CD,
∵AC=PC,
∴∠OAC=∠P.
∵∠BOC=2∠OAC,
∴∠BOC=2∠P.
∴∠P=30°.
∴2OC=OB+PB.
∴OB=3.
∵M为
的中点,
∴OM⊥AB.
∵∠MON=∠MCD=90°,∠NMO=∠DMC,
∴△MNO∽△MDC.
∴
=
.
即MN•MC=MO•MD=3×6=18.

∴∠ACB=90°.
∵∠COB=2∠PCB,∠BOC=2∠OAC,
∴∠CAB=∠BCP.
∴∠PCO=90°.
∴PC是⊙O的切线.
(2)由题意知,M为
 |
| AMB |
过M作⊙O的直径MD,连接CD,
∵AC=PC,
∴∠OAC=∠P.
∵∠BOC=2∠OAC,
∴∠BOC=2∠P.
∴∠P=30°.
∴2OC=OB+PB.
∴OB=3.
∵M为
 |
| AMB |
∴OM⊥AB.
∵∠MON=∠MCD=90°,∠NMO=∠DMC,
∴△MNO∽△MDC.
∴
| MN |
| MD |
| MO |
| MC |
即MN•MC=MO•MD=3×6=18.


练习册系列答案
相关题目
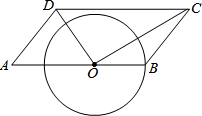
 交于点Q,过点C的切线CD交PQ于D,连接OC.
交于点Q,过点C的切线CD交PQ于D,连接OC.