题目内容
【题目】如图,将矩形纸片ABCD折叠,使点B与点D重合,折痕为MN,若AB=2,BC=4,那么线段MN的长为( ) 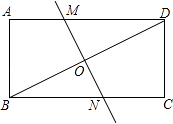
A.![]()
B.![]()
C.![]()
D.2 ![]()
【答案】B
【解析】解:如图,连接BM,DN
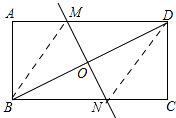
在矩形纸片ABCD中,CD=AB=2,∠C=90°,
在Rt△BCD中,BC=4,
根据勾股定理得,BD= ![]() =2
=2 ![]() ,
,
∴OB= ![]() BD=
BD= ![]() ,
,
由折叠得,∠BON=90°,ON= ![]() MN,BN=DN,
MN,BN=DN,
∵BC=BN+CN=4,
∴CN=4﹣BN,
在Rt△CDN中,CD=2,
根据勾股定理得,CN2+CD2=DN2,
(4﹣BN)2+22=BN2,
∴BN= ![]() ,
,
在Rt△BON中,ON= ![]() =
= ![]() ,
,
∴MN=2ON= ![]() ,
,
故选B.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数 | 频率 |
篮球 | 30 | 0.25 |
羽毛球 | m | 0.20 |
乒乓球 | 36 | n |
跳绳 | 18 | 0.15 |
其他 | 12 | 0.10 |
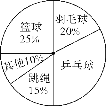
请根据以上图表信息,解答下列问题:
(1)频数分布表中的m=_________,n=_________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为_________.