题目内容
【题目】给出三个多项式:![]() x2+x-1,
x2+x-1,![]() x2+3x+1,
x2+3x+1,![]() x2+x,请你选择其中两个进行加法运算,并把结果因式分解.
x2+x,请你选择其中两个进行加法运算,并把结果因式分解.
【答案】答案见解析.
【解析】
试题因式分解的一般步骤是:1.提公因式;2.公式法(平方差公式的逆用a2- b2=(a+b)(a-b)和完全平方公式的逆用a2±2ab+b2= (a±b)2);3.十字相乘法,如选择:![]() x2+x-1,
x2+x-1,![]() x2+3x+1,则:
x2+3x+1,则:![]() x2+x-1+
x2+x-1+![]() x2+3x+1=x2+4x
x2+3x+1=x2+4x
=x(x+4);如选择:![]() x2-x,
x2-x,![]() x2+x-1,则:
x2+x-1,则:![]() x2-x+
x2-x+![]() x2+x-1= x2-1=(x+1)(x-1);如选择:
x2+x-1= x2-1=(x+1)(x-1);如选择:![]() x2-x ,
x2-x ,![]() x2+3x+1,则:
x2+3x+1,则:![]() x2-x +
x2-x +![]() x2+3x+1= x2+2x+1=(x+1)2.
x2+3x+1= x2+2x+1=(x+1)2.
试题解析:如选择:![]() x2+x-1,
x2+x-1,![]() x2+3x+1,则:
x2+3x+1,则:![]() x2+x-1+
x2+x-1+![]() x2+3x+1=x2+4x=x(x+4);
x2+3x+1=x2+4x=x(x+4);
如选择:![]() x2-x,
x2-x,![]() x2+x-1,则:
x2+x-1,则:![]() x2-x+
x2-x+![]() x2+x-1= x2-1=(x+1)(x-1);
x2+x-1= x2-1=(x+1)(x-1);
如选择:![]() x2-x ,
x2-x ,![]() x2+3x+1,则:
x2+3x+1,则:![]() x2-x +
x2-x +![]() x2+3x+1= x2+2x+1=(x+1)2.
x2+3x+1= x2+2x+1=(x+1)2.

【题目】某工厂甲、乙两个部门各有员工400人,为了解这两个部门员工的生产技能情况,进行了抽样调查,过程如下,请补充完整.
收集数据
从甲、乙两个部门各随机抽取20名员工,进行了生产技能测试,测试成绩(百分制)如下:
甲 78 86 74 81 75 76 87 70 75 90
75 79 81 70 74 80 86 69 83 77
乙 93 73 88 81 72 81 94 83 77 83
80 81 70 81 73 78 82 80 70 40
整理、描述数据
按如下分数段整理、描述这两组样本数据:

(说明:成绩80分及以上为生产技能优秀,70-79分为生产技能良好,60-69分为生产技能合格,60分以下为生产技能不合格)
分析数据
两组样本数据的平均数、中位数、众数如下表所示:
部门 | 平均数 | 中位数 | 众数 |
甲 | 78.3 | 77.5 | 75 |
乙 | 78 | 80.5 | 81 |
得出结论:
a.估计乙部门生产技能优秀的员工人数为________;
b.可以推断出________部门员工的生产技能水平较高,理由为________.(至少从两个不同的角度说明推断的合理性)
【题目】某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球、乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
运动项目 | 频数 | 频率 |
篮球 | 30 | 0.25 |
羽毛球 | m | 0.20 |
乒乓球 | 36 | n |
跳绳 | 18 | 0.15 |
其他 | 12 | 0.10 |
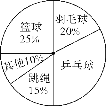
请根据以上图表信息,解答下列问题:
(1)频数分布表中的m=_________,n=_________;
(2)在扇形统计图中,“乒乓球”所在的扇形的圆心角的度数为_________.