Question

【题目】如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的C'处，点D落在点D'处，C'D'交线段AE于点G.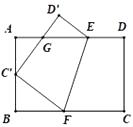

（1）求证：△BC'F∽△AGC'；
（2）若C'是AB的中点，AB=6，BC=9，求AG的长.

Answer 1

【答案】
（1）证明：∵四边形ABCD为矩形，且延AE折叠
∴∠A=∠B=∠GC'F=90°

∴∠BF C'+∠B C'F= 90°，∠A C'G+∠B C'F= 90°,

∴∠BF C'=∠A C'G

∴△BC'F∽△AGC'

（2）解：由勾股定理得 ，

∴BF=4.

∵ C'是AB的中点，AB=6，

∴AC'=BC'=3.

由（1）得△BC'F∽△AGC'，

∴ ，即

∴AG= .

【解析】（1）根据矩形的性质，和折叠前后对应角不变，得出△BC'F∽△AGC'
（2）根据折叠前后对应边长度相加等于原 长度，利用勾股定理求出BF的长，然后根据相似三角形对应边成比例，即可求出AG=