题目内容
【题目】如图,△ABC 中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.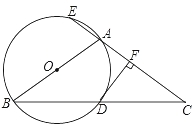
(1)求证:DF是⊙O的切线;
(2)若 ![]() ,半径OA=3,求AE的长.
,半径OA=3,求AE的长.
【答案】
(1)证明:连接OD,
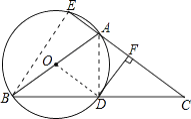
∵OB=OD,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DF⊥AC,
∴OD⊥DF,
∴DF是⊙O的切线
(2)解:连接BE,AD,∵AB是直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴∠ABC=∠C,BD=DC,
∵sinC= ![]() ,
,
∴sin∠ABC= ![]() ,
,
∵AB=2OA=6,
∴AD=2 ![]() ,
,
∴BD= ![]() ,
,
∴BC=2BD= ![]() ,
,
在Rt△BEC中,∵sinC= ![]() ,
,
∴BE= ![]() BC=
BC= ![]() ,
,
在Rt△ABE中,AE= ![]()
【解析】(1)要证切线可连接半径,证垂直,即证OD⊥DF即可;(2)出现直径时,连接BE,AD,构造出90度的圆周角,利用sinC的定义,求出BE,再利用勾股定理求出AE.
【考点精析】通过灵活运用切线的性质定理和切线的判定定理,掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线即可以解答此题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目