Question

【题目】如图1（注：与图2完全相同），二次函数y= x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0）两点，与y轴交于点C．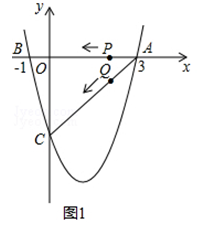

（1）求该二次函数的解析式；
（2）设该抛物线的顶点为D，求△ACD的面积（请在图1中探索）；
（3）若点P，Q同时从A点出发，都以每秒1个单位长度的速度分别沿AB，AC边运动，其中一点到达端点时，另一点也随之停止运动，当P，Q运动到t秒时，△APQ沿PQ所在的直线翻折，点A恰好落在抛物线上E点处，请直接判定此时四边形APEQ的形状，并求出E点坐标（请在图2中探索）．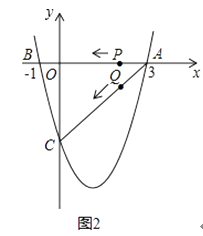

Answer 1

【答案】
（1）

解：∵二次函数y= x2+bx+c的图象与x轴交于A（3，0），B（﹣1，0），

∴ ，

解得： ，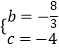

∴y= x2﹣ x﹣4

（2）

解：过点D作DM⊥y轴于点M，

∵y= x2﹣ x﹣4= （x﹣1）2﹣ ，

∴点D（1，﹣ ）、点C（0，﹣4），

则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC

= ×（1+3）× ﹣ ×（ ﹣4）×1﹣ ×3×4

=4

（3）

解：四边形APEQ为菱形，E点坐标为（﹣ ，﹣ ）．理由如下

如图2，E点关于PQ与A点对称，过点Q作，QF⊥AP于F，

∵AP=AQ=t，AP=EP，AQ=EQ

∴AP=AQ=QE=EP，

∴四边形AQEP为菱形，

∵FQ∥OC，

∴ = = ，

∴ = =

∴AF= t，FQ= t

∴Q（3﹣ t，﹣ t），

∵EQ=AP=t，

∴E（3﹣ t﹣t，﹣ t），

∵E在二次函数y= x2﹣ x﹣4上，

∴﹣ t= （3﹣ t）2﹣ （3﹣ t）﹣4，

∴t= ，或t=0（与A重合，舍去），

∴E（﹣ ，﹣ ）

【解析】（1）将A，B点坐标代入函数y= x2+bx+c中，求得b、c，进而可求解析式；（2）由解析式先求得点D、C坐标，再根据S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC ， 列式计算即可；（3）注意到P，Q运动速度相同，则△APQ运动时都为等腰三角形，又由A、E对称，则AP=EP，AQ=EQ，易得四边形四边都相等，即菱形．利用菱形对边平行且相等的性质可用t表示E点坐标，又E在二次函数的图象上，所以代入即可求t，进而E可表示．