��Ŀ����
����Ŀ���ŷ����Ǵ��ϲ����һ���˶��������������С�����������㳡�Ϸŷ��ݣ���ͼ������A����С���÷��ݹ�����һ�������ϣ����ݹ̶�����D������ʱ����AD��ˮƽ�ߵļн�Ϊ30�㣬Ϊ�˱��ڹ۲죬С��Ѹ����ǰ���ƶ������ߵ�������A��10��B������ʱ������BD��ˮƽ�ߵļн�Ϊ45�㣮��֪��A��B��C��ͬһ��ˮƽֱ���ϣ��������С����ʱ���ջصķ����ߵij����Ƕ����ף���������AD��BD��Ϊ�߶Σ� ![]() ��1.414��
��1.414�� ![]() ��1.732���������ȷ��1�ף���
��1.732���������ȷ��1�ף��� 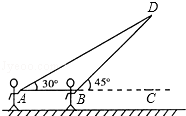
���𰸡��⣺��DH��BC��H����DH=x�ף� 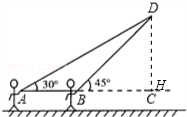
�ߡ�ACD=90�㣬
����ֱ�ǡ�ADH�У���DAH=30�㣬AD=2DH=2x��AH=DH��tan30��= ![]() x��
x��
��ֱ�ǡ�BDH�У���DBH=45�㣬BH=DH=x��BD= ![]() x��
x��
��AH��BH=AB=10�ף�
�� ![]() x��x=10��
x��x=10��
��x=5�� ![]() +1����
+1����
��С����ʱ���ջصķ��ݵij���Ϊ��
AD��BD=2x�� ![]() x=��2��
x=��2�� ![]() ����5��
����5�� ![]() +1���֣�2��1.414����5����1.732+1����8��
+1���֣�2��1.414����5����1.732+1����8��
����������DH��BC��H����DH=x�ף��������Ǻ�����ʾ��AH��BH�ij�������AH��BH=AB�õ�һ������x�ķ��̣��ⷽ�����x��ֵ���������AD��BD�ij������ɽ��⣮

��ϰ��ϵ�д�
�����Ŀ