Question

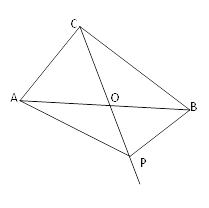
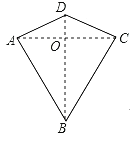
【题目】两组邻边相等的四边形叫做“筝形”，如图，四边形ABCD是一个筝形，其中 AB=CB,AD=CD,詹姆斯在探究筝形的性质时，得到如下结论：① ACBD；②AOCOAC；③△ABD≌△CBD；④四边形ABCD的面积=ACBD，其中，正确的结论有_____.

Answer 1

【答案】①②③④．

【解析】

先证明△ABD与△CBD全等，再证明△AOD与△COD全等即可判断．

在△ABD与△CBD中，

，

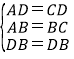∴△ABD≌△CBD（SSS），

故③正确；

∴∠ADB=∠CDB，

在△AOD与△COD中，

，

∴△AOD≌△COD（SAS），

∴∠AOD=∠COD=90°，AO=OC，

∴AC⊥DB，

故①②正确；

四边形ABCD的面积=S△ADB+S△BDC=DB×OA+DB×OC=ACBD，

故④正确；

故答案为①②③④．