题目内容
(本题满分14分,其中第(1)、(2)小题各4分,第(3)小题6分)已知:如图,在平面直角坐标系xOy中,二次函数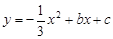 的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
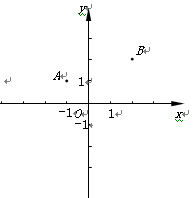
小题1:(1)求这个二次函数的解析式和它的对称轴;
小题2:(2)求证:∠ABO=∠CBO;
小题3:(3)如果点P在直线AB上,且△POB
与△BCD相似,求点P的坐标.
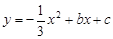 的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
的图像经过点A(-1,1)和点B(2,2),该函数图像的对称轴与直线OA、OB分别交于点C和点D.
小题1:(1)求这个二次函数的解析式和它的对称轴;
小题2:(2)求证:∠ABO=∠CBO;
小题3:(3)如果点P在直线AB上,且△POB
与△BCD相似,求点P的坐标.
小题1:(1)解:由题意,得
 ………………………………………(1分)
………………………………………(1分)解得
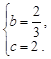 ………………………………………………………………(1分)
………………………………………………………………(1分)∴所求二次函数的解析式为
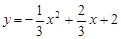 .……………………(1分)
.……………………(1分)对称轴为直线x=1.
小题2:(2)证明:由直线OA的表达式y=-x,得点C的坐标为(1,-1).…………(1分)
∵
 ,
,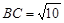 ,∴AB=BC.…………………………………(1分)
,∴AB=BC.…………………………………(1分)又∵
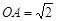 ,
,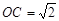 ,∴OA=OC.………………………………(1分)
,∴OA=OC.………………………………(1分)∴∠ABO=∠CBO.
小题3:(3)解:由直线OB的表达式y=x,得点D的坐标为(1,1).………………(1分)
由直线AB的表达式
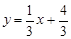 ,
,得直线与x轴的交点E的坐标为(-4,0).………………………………(1分)
∵△POB与△BCD相似,∠ABO=∠CBO,
∴∠BOP=∠BDC或∠BOP=∠BCD.
(i)当∠BOP=∠BDC时,由∠BDC==135°,得∠BOP=135°.
∴点P不但在直线AB上,而且也在x轴上,即点P与点E重合.
∴点P的坐标为(-4,0).…………………………………………………(2分)
(ii)当∠BOP=∠BCD时,
由△POB∽△BCD,得
 .
.而
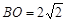 ,
,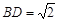 ,
,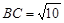 ,∴
,∴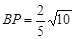 .
.又∵
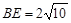 ,∴
,∴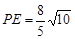 .
.作PH⊥x轴,垂足为点H,BF⊥x轴,垂足为点F.
∵PH∥BF,∴
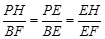 .
.而BF=2,EF=6,∴
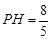 ,
,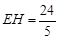 .
.∴
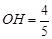 .
.∴点P的坐标为(
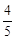 ,
, ).………………………………………………(2分)
).………………………………………………(2分)综上所述,点P的坐标为(-4,0)或(
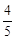 ,
, )
)略

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
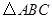 中,
中,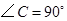 ,在
,在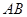 边上取一点
边上取一点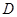 ,使
,使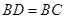 ,过
,过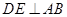 交AC于E,AC=8,BC=6.求DE的长.
交AC于E,AC=8,BC=6.求DE的长.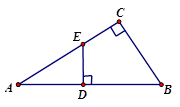
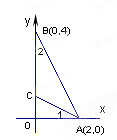
 中,点
中,点 分别在边
分别在边 上,
上,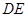 ∥
∥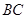 ,
,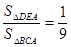 ,
,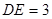 ,那么
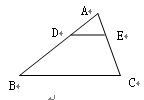
,那么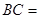 ▲ .
▲ .
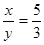 ,那么
,那么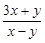 = ▲ .
= ▲ .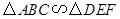 ,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为
,相似比为1∶2,且△ABC的面积为4,则△DEF的面积为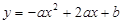 与x轴的一个交点为A(-1,0),与y轴正半轴交于点C.
与x轴的一个交点为A(-1,0),与y轴正半轴交于点C.
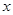 轴的另一个交点B的坐标;
轴的另一个交点B的坐标; ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2. E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设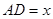 ,
,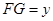 ,
,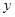 关于
关于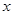 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域; 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
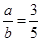 ,那么
,那么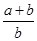 等于 .
等于 .