题目内容
【题目】如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A,B两点.
(1)则点A,B,C的坐标分别是A( , ),B( , ),C( , );
(2)设经过A,B两点的抛物线解析式为y=![]() (x﹣5)2+k,它的顶点为E,求证:直线EA与⊙M相切;
(x﹣5)2+k,它的顶点为E,求证:直线EA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】
(1)2;0;8;0;0;4
(2)
证明:把点A(2,0)代入抛物线y=![]() (x﹣5)2+k,
(x﹣5)2+k,
得:k=﹣![]() ,
,
∴E(5,﹣![]() ),
),
∴DE=![]() ,
,
∴ME=MD+DE=4+![]() =
=![]() ,EA2=32+(
,EA2=32+(![]() )2=
)2=![]() ,
,
∵MA2+EA2=52+![]() =
=![]() ,ME2=
,ME2=![]() ,
,
∴MA2+EA2=ME2,
∴∠MAE=90°,
即EA⊥MA,
∴EA与⊙M相切;
(3)
解:存在;点P坐标为(5,4),或(5,![]() ),或(5,4+
),或(5,4+![]() );理由如下:
);理由如下:
由勾股定理得:BC=![]() ,
,
分三种情况:
①当PB=PC时,点P在BC的垂直平分线上,点P与M重合,
∴P(5,4);
②当BP=BC=4![]() 时,如图2所示:
时,如图2所示:
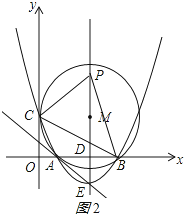
∵PD=![]() =
=![]() =
=![]() ,
,
∴P(5,![]() );
);
③当PC=BC=4![]() 时,连接MC,如图3所示:
时,连接MC,如图3所示:
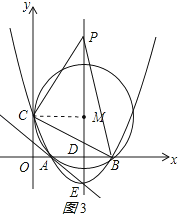
则∠PMC=90°,
根据勾股定理得:PM=![]() ,
,
∴PD=4+![]() ,
,
∴P(5,4+![]() );
);
综上所述:存在点P,且点P在x轴的上方,使△PBC是等腰三角形,
点P的坐标为(5,4),或(5,![]() ),或(5,4+
),或(5,4+![]() ).
).
【解析】(1)连接MC、MA,由切线的性质得出MC⊥y轴,MC=MA=5,OC=MD=4,得出点C的坐标;由MD⊥AB,得出DA=DB,∠MDA=90°,由勾股定理求出AD,得出BD、OA、OB,即可得出点A、B的坐标;
(2)把点A(2,0)代入抛物线得出k=﹣![]() ,得出顶点E的坐标,得出DE、ME,由勾股定理得出EA2=
,得出顶点E的坐标,得出DE、ME,由勾股定理得出EA2=![]() ,证出MA2+EA2=ME2 , 由勾股定理的逆定理证出∠MAE=90°,即可得出EA与⊙M相切;
,证出MA2+EA2=ME2 , 由勾股定理的逆定理证出∠MAE=90°,即可得出EA与⊙M相切;
(3)由勾股定理求出BC,分三种情况:①当PB=PC时,点P在BC的垂直平分线上,点P与M重合,容易得出点P的坐标;
②当BP=BC=4![]() 时,由勾股定理求出PD,即可得出点P的坐标;
时,由勾股定理求出PD,即可得出点P的坐标;
③当PC=BC=4![]() 时,由勾股定理求出PM,得出PD,即可得出点P的坐标.
时,由勾股定理求出PM,得出PD,即可得出点P的坐标.

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案