Question

【题目】如图，反比例函数y= 的图象与一次函数y=k2x+b的图象交于点P（m，﹣1）和Q（1，2）两点，记一次函数与坐标轴的交点分别为A，B，连接OP，OQ．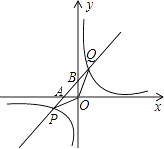
（1）求两函数的解析式；
（2）求证：△POB≌△QOA．

Answer 1

【答案】
（1）解：将Q（1，2）代入反比例函数 ，得k1=2

∴反比例函数的解析式为

将P（m，﹣1）代入反比例函数 ，得m=﹣2

∴P（﹣2，﹣1）

将P（﹣2，﹣1）和Q（1，2）代入一次函数y=k2x+b，得

解得

∴该一次函数的解析式为y=x+1

（2）解：∵y=x+1，当x=0时，y=1；当y=0时，x=﹣1

∴A（﹣1，0），B（0，1）

∴OA=OB

∴∠QAO=∠PBO

∵OP= = ，OQ= =

∴OP=OQ

∴∠BPO=∠AQO

∴△POB≌△QOA（AAS）

【解析】（1）将已知的点Q的坐标代入反比例函数，求得比例系数k1的值，得到反比例函数解析式；再将点P的坐标代入反比例函数，求得m的值，最后将点P和点Q的坐标代入一次函数，求得k2和b的值，得到一次函数解析式；（2）先根据一次函数求得直线与与坐标轴的交点A、B的坐标，进而根据OA和OB的长相等，得到∠QAO=∠PBO；再根据点P、Q的坐标，求得OP与OQ的长，根据OP与OQ的长相等，得到∠BPO=∠AQO，最后根据AAS得到△POB≌△QOA．
【考点精析】本题主要考查了确定一次函数的表达式的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能正确解答此题．