Question

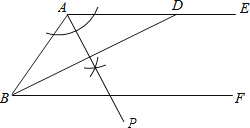
【题目】如图，已知BD平分∠ABF，且交AE于点D，

（1）求作：∠BAE的平分线AP（要求：尺规作图，保留作图痕迹，不写作法）；
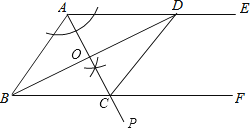
（2）设AP交BD于点O，交BF于点C，连接CD，当AC⊥BD时，求证：四边形ABCD是菱形．

Answer 1

【答案】
（1）

解：如图所示：

（2）

证明：如图：

在△ABO和△CBO中，

，

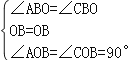∴△ABO≌△CBO（ASA），

∴AO=CO，AB=CB．

在△ABO和△ADO中，

，

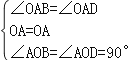∴△ABO≌△ADO（ASA），

∴BO=DO．

∵AO=CO，BO=DO，

∴四边形ABCD是平行四边形，

∵AB=CB，

∴平行四边形ABCD是菱形．

【解析】此题考查了基本作图，涉及知识点有全等三角形以及平行四边形和菱形的判定方法.
【考点精析】本题主要考查了菱形的判定方法的相关知识点，需要掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形才能正确解答此题．