题目内容
【题目】函数y=ax2+bx+a+b(a≠0)的图象可能是()
A. 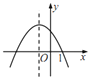 B.
B. 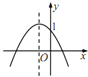
C. 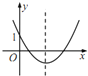 D.
D. 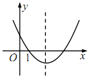
【答案】C
【解析】
根据各选项中函数的图像可以得到a、b、c的关系,从而可以判断各选项中那个函数图像可能是正确的.
解: A:由图像可知,开口向下,则a<0,又因为顶点在y轴左侧,则b<0,则a+b<0,而图像与y轴交点为(0,a+b)在y轴正半轴,与a+b<0矛盾故此选项错误;
B:由图像可知,开口向下,则a<0,又因为顶点在y轴左侧,则b<0,则a+b<0,而图像与y轴交点为(0,1)在y轴正半轴,可知a+b=1与a+b<0矛盾,故此选项错误;
C:由图像可知开口向上,则a>0,顶点在y轴右侧,则b<0,a+b=1,故此选项正确;
D:由图像可知开口向上则a>0,顶点在y轴右侧,则b<0,与y轴交于正半轴则a+b>0,而图像与x轴的交点为(1,0),则a+b+a+b=0,即a+b=0与a+b>0矛盾,故此选项错误;
故选C.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目