题目内容
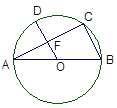
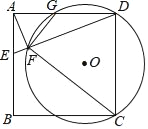
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
【答案】(1)详见解析;(2)⊙O的半径为![]() .
.
【解析】
(1)欲证明△AFG∽△DFC,只要证明∠FAG=∠FDC,∠AGF=∠FCD;
(2)首先证明CG是直径,求出CG即可解决问题;
(1)证明:在正方形ABCD中,∠ADC=90°,
∴∠CDF+∠ADF=90°,
∵AF⊥DE,
∴∠AFD=90°,
∴∠DAF+∠ADF=90°,
∴∠DAF=∠CDF,
∵四边形GFCD是⊙O的内接四边形,
∴∠FCD+∠DGF=180°,
∵∠FGA+∠DGF=180°,
∴∠FGA=∠FCD,
∴△AFG∽△DFC.
(2)解:如图,连接CG.
∵∠EAD=∠AFD=90°,∠EDA=∠ADF,
∴△EDA∽△ADF,
∴![]() ,即
,即![]() ,
,
∵△AFG∽△DFC,
∴![]() ,
,
∴![]() ,
,
在正方形ABCD中,DA=DC,
∴AG=EA=1,DG=DA﹣AG=4﹣1=3,
∴CG=![]() =5,
=5,
∵∠CDG=90°,
∴CG是⊙O的直径,
∴⊙O的半径为![]() .
.

练习册系列答案
相关题目
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.