Question

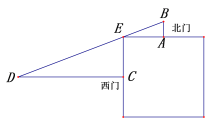
【题目】我国古代数学著作《九章算术》中记载了一个问题：“今有邑方不知大小，各开中门，出北门三十步有木，出西门七百五十步见木，问：邑方几何？” .其大意是:如图，一座正方形城池，A为北门中点，从点A往正北方向走30步到B出有一树木，C为西门中点，从点C往正西方向走750步到D处正好看到B处的树木，求正方形城池的边长.

Answer 1

【答案】正方形城池的边长为300步

【解析】

本题只要是把实际问题抽象到相似三角形中，利用相似三角形的对应边成比例，列出方程，通过解方程即可求出小城的边长．

依题意得AB=30步，CD=750步.

设AE为x步，则正方形边长为2x步，根据题意，

Rt△ABE∽Rt△CED

∴ 即.

解得x1=150，x2=-150（不合题意，舍去），

∴2x=300

∴正方形城池的边长为300步.