题目内容
【题目】如图,抛物线y=﹣![]() x2+
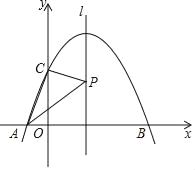
x2+![]() x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
x+2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,P为此抛物线对称轴l上任意一点,则△APC的周长的最小值是( )
A. 2![]() B. 3
B. 3![]() C. 5
C. 5![]() D.
D. ![]() +
+![]()
【答案】B
【解析】
作点C关于直线l的对称点C′,连接AC′交直线l于P,连接PC,则△APC的周长的最小,根据抛物线的对称性、二次函数与一元二次方程的关系计算即可.
作点C关于直线l的对称点C′,连接AC′交直线l于P,连接PC,则△APC的周长的最小,
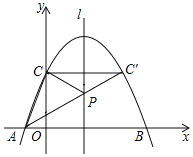
由抛物线的对称性可知,点C′在抛物线上,
当x=0时,y=2,
∴点C的坐标为(0,2),
∴点C′的纵坐标为2,
2=﹣![]() x2+
x2+![]() x+2,
x+2,
解得,x1=0,x2=3,
则点C′的横坐标为3,
﹣![]() x2+
x2+![]() x+2=0,
x+2=0,
x1=-1,x2=4,
则点A的坐标为(-1,0),
∴AC′=![]() =2
=2![]() ,AC=
,AC=![]() =
=![]() ,
,
∴△APC的周长的最小值是3![]() ,
,
故选:B.

练习册系列答案
相关题目
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
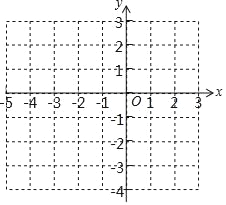
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.