Question

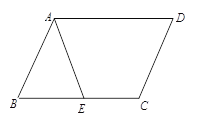
【题目】如图，在平面直角坐标系中，ABCO的顶点A、C的坐标分别为A(2,0)、C(－1,2)，反比例函数y＝(k≠0)的图象经过点B.

(1)直接写出点B坐标．

(2)求反比例函数的表达式．

Answer 1

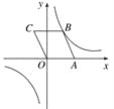
【答案】(1) B的坐标为(1,2);(2) y＝.

【解析】

（1）设BC与y轴的交点为F，过点B作BE⊥x轴于E，如图，易证△CFO≌△AEB，从而可得到点B的坐标；

（2）运用待定系数法就可解决问题．

（1）设BC与y轴的交点为F，过点B作BE⊥x轴于E，如图，∵ABCO的顶点A、C的坐标分别为A（2，0）、C（﹣1，2），∴CF=1，OF=2，OA=2，OC=BA，∠C=∠EAB，∠CFO=∠AEB=90°．

在△CFO和△AEB中，∵，∴△CFO≌△AEB，∴CF=AE=1，OF=BE=2，∴OE=OA﹣AE=2﹣1=1，∴点B的坐标为（1，2）．

（2）∵反比例函数y（k≠0）的图象经过点B，∴k=1×2=2，∴反比例函数的表达式为．