题目内容
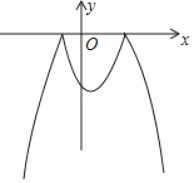
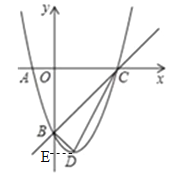
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状.
【答案】(1)y=x2-2x-3;(2)C(3,0),D(1,-4),△BCD是直角三角形.
【解析】
(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论.
(1)∵x2+4x+3=0,∴x1=﹣1,x2=﹣3.
∵m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3.
∵抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴抛物线解析式为y=x2﹣2x﹣3;
,∴抛物线解析式为y=x2﹣2x﹣3;
(2)令y=0,则x2﹣2x﹣3=0,∴x1=﹣1,x2=3,∴C(3,0).
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,∴顶点坐标D(1,﹣4).
过点D作DE⊥y轴.
∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形.

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.