题目内容
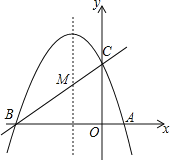
【题目】已知二次函数y=﹣x2+x+6及一次函数y=x+m,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=x+m与这个新图象有四个交点时,m的取值范围是_____.
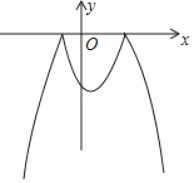
【答案】﹣7<m<﹣3.
【解析】
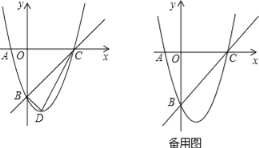
如图,解方程﹣x2+x+6=0得A(﹣2,0),B(3,0),再利用折叠的性质求出折叠部分的解析式为y=(x+2)(x﹣3),即y=x2﹣x﹣6(﹣2≤x≤3),然后求出直线y=x+m经过点A(﹣2,0)时m的值和当直线y=x+m与抛物线y=x2﹣x﹣6(﹣2≤x≤3)有唯一公共点时m的值,从而得到当直线y=x+m与新图象有4个交点时,m的取值范围.
解:如图所示,过点B作直线y=x+m1,将直线向下平移到恰在点C处相切,
则一次函数y=x+m在两条直线之间时,两个图象有4个交点,
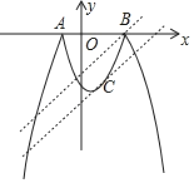
令y=﹣x2+x+6=0,解得:x=﹣2或3,即点B坐标(3,0),
翻折抛物线的表达式为:y=(x﹣3)(x+2)=x2﹣x﹣6(﹣2≤x≤3),
将一次函数与二次函数表达式联立并整理得:x2﹣2x﹣6﹣m=0,
△=b2﹣4ac=4+4(6+m)=0,解得:m=﹣7,
当一次函数过点B时,将点B坐标代入:y=x+m得:0=3+m,解得:m=﹣3,
所以当直线y=x+m与这个新图象有四个交点时,m的取值范围是﹣7<m<﹣3.

练习册系列答案
相关题目