题目内容
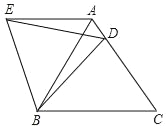
【题目】已知抛物线C1:y1=a(x﹣h)2+2,直线1:y2=kx﹣kh+2(k≠0).
(1)求证:直线l恒过抛物线C的顶点;
(2)若a>0,h=1,当t≤x≤t+3时,二次函数y1=a(x﹣h)2+2的最小值为2,求t的取值范围.
(3)点P为抛物线的顶点,Q为抛物线与直线l的另一个交点,当1≤k≤3时,若线段PQ(不含端点P,Q)上至少存在一个横坐标为整数的点,求a的取值范围.
【答案】(1)证明见解析;(2)﹣2≤t≤1;(3)﹣1<a<0或0<a<1.
【解析】
(1)利用二次函数的性质找出抛物线的顶点坐标,将x=h代入一次函数解析式中可得出点(h,2)在直线1上,进而可证出直线l恒过抛物线C1的顶点;
(2)由a>0可得出当x=h=1时y1=a(x﹣h)2+2取得最小值2,结合当t≤x≤t+3时二次函数y1=a(x﹣h)2+2的最小值为2,可得出关于t的一元一次不等式组,解之即可得出结论;
(3)令y1=y2可得出关于x的一元二次方程,解之可求出点P,Q的横坐标,由线段PQ(不含端点P,Q)上至少存在一个横坐标为整数的点,可得出![]() >1或
>1或![]() <﹣1,再结合1≤k≤3,即可求出a的取值范围.
<﹣1,再结合1≤k≤3,即可求出a的取值范围.
(1)∵抛物线C1的解析式为y1=a(x﹣h)2+2,
∴抛物线的顶点为(h,2),
当x=h时,y2=kx﹣kh+2=2,
∴直线l恒过抛物线C1的顶点;
(2)∵a>0,h=1,
∴当x=1时,y1=a(x﹣h)2+2取得最小值2,
又∵当t≤x≤t+3时,二次函数y1=a(x﹣h)2+2的最小值为2,
∴![]() ,
,
∴﹣2≤t≤1;
(3)令y1=y2,则a(x﹣h)2+2=k(x﹣h)+2,
解得:x1=h,x2=h+![]() ,
,
∵线段PQ(不含端点P,Q)上至少存在一个横坐标为整数的点,
∴![]() >1或
>1或![]() <﹣1,
<﹣1,
∵k>0,
∴0<a<k或﹣k<a<0,
又∵1≤k≤3,
∴﹣1<a<0或0<a<1.

【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④