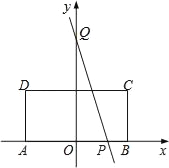
题目内容
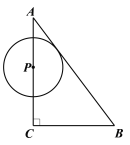
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 运动,速度为
运动,速度为![]() 个单位/
个单位/![]() ,在点
,在点![]() 运动的过程中,以
运动的过程中,以![]() 为圆心的圆始终与斜边
为圆心的圆始终与斜边![]() 相切,设⊙
相切,设⊙![]() 的面积为
的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() (
(![]() )(
)(![]() ).
).
(1)当![]() 时,
时,![]() ;(用含
;(用含![]() 的式子表示)
的式子表示)
(2)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,直接写出t的值.
【答案】(1)7-t(2)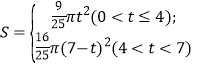 (3)
(3)![]()
【解析】
(1)先判断出点P在BC上,即可得出结论;
(2)分点P在边AC和BC上两种情况:利用相似三角形的性质得出比例式建立方程求解即可得出结论;
(3)分点P在边AC和BC上两种情况:借助(2)求出的圆P的半径等于PC,建立方程求解即可得出结论.
(1)∵AC=4,BC=3,∴AC+BC=7.
∵4<t<7,∴点P在边BC上,∴BP=7﹣t.
故答案为:7﹣t;
(2)在Rt△ABC中,AC=4,BC=3,根据勾股定理得:AB=5,由运动知,AP=t,分两种情况讨论:
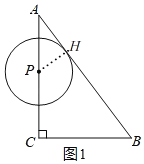
①当点P在边AC上时,即:0<t≤4,如图1,记⊙P与边AB的切点为H,连接PH,∴∠AHP=90°=∠ACB.
∵∠A=∠A,∴△APH∽△ACB,∴![]() ,∴
,∴![]() ,∴PH
,∴PH![]() t,∴S
t,∴S![]() πt2;
πt2;
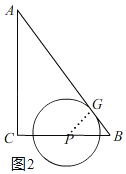
②当点P在边BC上时,即:4<t<7,如图,记⊙P与边AB的切点为G,连接PG,∴∠BGP=90°=∠C.
∵∠B=∠B,∴△BGP∽△BCA,∴![]() ,∴
,∴![]() ,∴PG
,∴PG![]() (7﹣t),∴S
(7﹣t),∴S![]() π(7﹣t)2.
π(7﹣t)2.
综上所述:S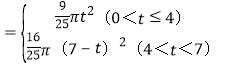 ;
;
(3)分两种情况讨论:
①当点P在边AC上时,即:0<t≤4,由(2)知,⊙P的半径PH![]() t.
t.
∵⊙P与△ABC的另一边相切,即:⊙P和边BC相切,∴PC=PH.
∵PC=4﹣t,∴4﹣t![]() t,∴t
t,∴t![]() 秒;
秒;
②当点P在边BC上时,即:4<t<7,由(2)知,⊙P的半径PG![]() (7﹣t).
(7﹣t).
∵⊙P与△ABC的另一边相切,即:⊙P和边AC相切,∴PC=PG.
∵PC=t﹣4,∴t﹣4![]() (7﹣t),∴t
(7﹣t),∴t![]() 秒.
秒.
综上所述:在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,t的值为![]() 秒或
秒或![]() 秒.
秒.

【题目】表中所列 ![]() 的7对值是二次函数
的7对值是二次函数![]() 图象上的点所对应的坐标,其中
图象上的点所对应的坐标,其中 ![]()
x | … |
|
|
|
|
|
|
| … |
y | … | 7 | m | 14 | k | 14 | m | 7 | … |
根据表中提供的信息,有以下4 个判断:
① ![]() ;②
;② ![]() ;③ 当
;③ 当![]() 时,y 的值是 k;④
时,y 的值是 k;④ ![]() 其中判断正确的是 ( )
其中判断正确的是 ( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④