题目内容
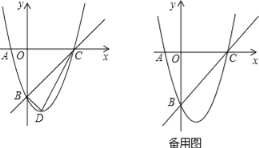
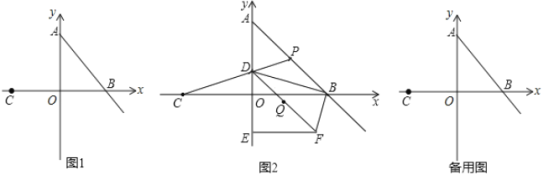
【题目】如图1，在平面直角坐标系中，
为坐标原点，点
的坐标为
，点
的坐标为
，点
的坐标为
，
（1）求直线
的函数解析式；
（2）如图2，点
在线段（不包括，两点）上，连接
与
轴交于点
，连接
．
、
的垂直平分线交于点
，连接
并延长到点
，使
，作
轴于
，连结
．求证：
；
（3）在（2）的条件下，当
的边
时，求点的坐标．
【答案】（1）
；（2）见解析；（3）点
的坐标为
．
【解析】
（1）设直线
的函数解析式为
，把
代入即可；
（2）作辅助线，如图2，根据
作圆
，证明
也在圆上，证出
，得出
，再根据
，即可得出
，连接
，根据
，
，
，
，得出
，再证出
，最后根据
，得出
是等腰直角三角形，从而求出结论；
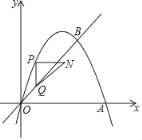
（3）如图3，过点
作
于点
，则
，再证出
，得比例式，得出
，
，再根据
，得出四边形
是矩形，
，
，根据
，求出
的长，从而得出直线
的解析式，最后根据方程的解可得的坐标．
解：（1）
点
的坐标为
，
设直线的函数解析式为，
代入得：
，
解得：
，
则直线的函数解析式为
；
（2）如图2，连接
，
，
、
的垂直平分线交于点，
，
以为圆心，以
为半径作
，
是直径，
轴，
，
在上，
由已知得：
，
，
又
，
，
，
，
，
连接
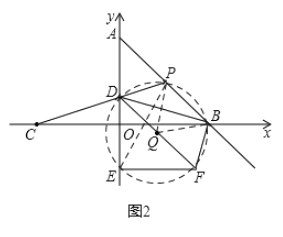
是
的一个外角，
，
是
的一个外角，
，
，，
，
，
，
，
，
，
，
是等腰直角三角形，
；
（3）如图3，过点作于点，
，
，
，
又
，
，
，
，，
，
四边形是矩形，
，
，
，
，
解得：
，
点
的坐标为
，
直线的解析式为
，
由直线的函数解析式为；
得
解得：
，
则点的坐标为
．
练习册系列答案
阅读快车系列答案
相关题目
