题目内容
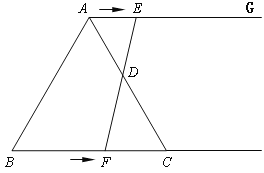
【题目】如图,在等边三角形ABC中,BC=6cm. 射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空:当t为_________s时,四边形ACFE是菱形;
【答案】(1)证明见解析(2)①6②1.5
【解析】试题分析:(1)由题意得到AD=CD,再由AG与BC平行,利用两直线平行内错角相等得到两对角相等,利用AAS即可得证;
(2)①若四边形ACFE是菱形,则有CF=AC=AE=6,由E的速度求出E运动的时间即可;
②分两种情况考虑:若CE⊥AG,此时四点构成三角形,不是直角梯形;若AF⊥BC,求出BF的长度及时间t的值.
(1)证明:∵AG∥BC,
∴∠EAD=∠DCF,∠AED=∠DFC,
∵D为AC的中点,
∴AD=CD,
∵在△ADE和△CDF中,
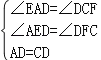 ,
,
∴△ADE≌△CDF(AAS);
(2)解:①若四边形ACFE是菱形,则有CF=AC=AE=6,
则此时的时间t=6÷1=6(s);
②四边形AFCE为直角梯形时,
(I)若CE⊥AG,则AE=3,BF=3×2=6,即点F与点C重合,不是直角梯形.
(II)若AF⊥BC,
∵△ABC为等边三角形,
∴F为BC中点,即BF=3,
∴此时的时间为3÷2=1.5(s);
故答案为:6;1.5.

练习册系列答案
相关题目