题目内容
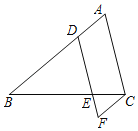
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.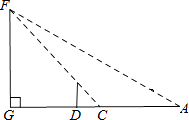
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,结果精确到0.1)
,结果精确到0.1)
【答案】
(1)解:∵由题意知,FG∥DE,
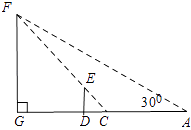
∴△CDE∽△CGF,
∴ ![]() ,即
,即 ![]() ,
,
∴ ![]()
(2)解:在直角△AFG中,∠A=30°, ![]() ,
,
∵tanA= ![]() ,tan30°=
,tan30°= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得FG≈12.5.
答:电线杆PQ的高度约12.5米.
【解析】(1)根据平行于三角形一边的直线截其他两边,所截得的三角形与原三角形相似,判断出△CDE∽△CGF,然后根据相似三角形对应边成比例得出![]() =
=![]() ,从而用a表示出GD;
,从而用a表示出GD;
(2)在直角△AFG中,∠A=30°, A G = ![]() F G + 6 ,根据
F G + 6 ,根据![]() A的正切等于tan30°,从而列出方程求解即可得出FG的长.
A的正切等于tan30°,从而列出方程求解即可得出FG的长.
【考点精析】本题主要考查了相似三角形的判定与性质和锐角三角函数的定义的相关知识点,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目