题目内容
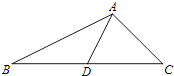
【题目】如图,AB=AC,AC的垂直平分线MN交AB于D,交AC于E.

(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD的周长17,求△ABC的周长.
【答案】(1) 30°;(2) 27.
【解析】
试题(1)先根据等腰角形的性质求出∠B=∠ACB=![]() =70°,再由MN垂直平分线AC可知AD=CD,所以∠ACD=∠A,再根据∠BCD=∠ACB-∠ACD即可得出结论;
=70°,再由MN垂直平分线AC可知AD=CD,所以∠ACD=∠A,再根据∠BCD=∠ACB-∠ACD即可得出结论;
(2)由MN是AC的垂直平分线可知,AD=DC,AC=2AE,所以AB=AC,再由△BCD的周长=BC+CD+BD=AB+BC=17,可知求出△ABC的周长.
试题解析:(1)∵AB=AC
∴∠B=∠ACB=![]() =70°,
=70°,
∵MN垂直平分线AC
∴AD=CD,
∴∠ACD=∠A=40°,
∴∠BCD=∠ACB-∠ACD=70°-40°=30°;
(2)∵MN是AC的垂直平分线
∴AD=DC,AC=2AE=10,
∴AB=AC=10,
∵△BCD的周长=BC+CD+BD=AB+BC=17,
∴△ABC的周长=AB+BC+AC=17+10=27.

练习册系列答案
相关题目