题目内容
【题目】如图,AB∥CD,∠A=50°,∠C=45°,求∠P的度数.
下面提供三种思路:
(1)过P作FG∥AB
(2)延长AP交直线CD于M;
(3)延长CP交直线AB于N.
请选择两种思路,求出∠P的度数.
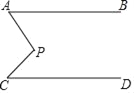
【答案】∠APC=95°,方法见解析.
【解析】
(1)过P作PG∥AB,利用平行线的性质以及三角形外角性质进行计算即可.
(2)延长AP交直线CD于M,利用平行线的性质以及三角形外角性质进行计算即可.
(3)延长CP交直线AB于N,利用平行线的性质以及三角形外角性质进行计算即可.
解:(1)过P作PG∥AB,
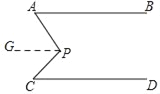
∵AB∥CD,
∴AB∥CD∥PG,
∴∠A=∠APG,∠C=∠CPG,
∴∠APC=APG+∠CPG=∠A+∠C=50°+45°=95°;
(2)延长AP交直线CD于M;
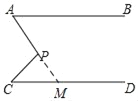
∵AB∥CD,
∴∠A=∠AMC=50°,
又∵∠C=45°,
∴∠APC=∠AMC+∠C=50°+45°=95°;
(3)延长CP交直线AB于N.
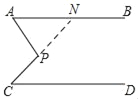
∵AB∥CD,
∴∠C=∠ANC=45°,
又∵∠A=50°,
∴∠APC=∠ANC+∠A=45°+50°=95°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目