题目内容
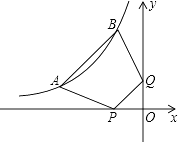
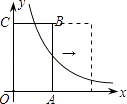
【题目】如图，矩形OABC的两条边在坐标轴上，OA=1，OC=2，现将此矩形向右平移，每次平移1个单位，若第1次平移得到的矩形的边与反比例函数图象有两个交点，它们的纵坐标之差的绝对值为0.6，则第n次（n＞1）平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为（用含n的代数式表示）
【答案】
或 
【解析】解：设反比例函数解析式为y= 
，则
①与BC，AB平移后的对应边相交；
与AB平移后的对应边相交的交点的坐标为（2，1.4），
则1.4= 
，
解得k=2.8= 
，
故反比例函数解析式为y= 
．
则第n次（n＞1）平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为： 
﹣ 
= ；
②与OC，AB平移后的对应边相交；
k﹣ =0.6，
解得k= 
．
故反比例函数解析式为y= 
．
则第n次（n＞1）平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为： 
﹣ 
= 
．
故第n次（n＞1）平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为 或 ．
所以答案是： 或 ．
【考点精析】掌握反比例函数的性质是解答本题的根本，需要知道性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．
练习册系列答案
相关题目
