题目内容
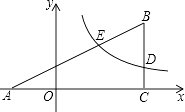
【题目】如图，在平面直角坐标系xOy中，抛物线y=ax2+bx+c交y轴于点C（0，4），对称轴x=2与x轴交于点D，顶点为M，且DM=OC+OD．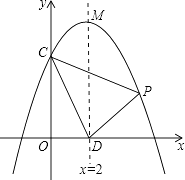
（1）求该抛物线的解析式；
（2）设点P（x，y）是第一象限内该抛物线上的一个动点，△PCD的面积为S，求S关于x的函数关系式，并写出自变量x的取值范围；
（3）在（2）的条件下，若经过点P的直线PE与y轴交于点E，是否存在以O、P、E为顶点的三角形与△OPD全等？若存在，请求出直线PE的解析式；若不存在，请说明理由．
【答案】
（1）
解：由题意得：OC=4，OD=2，
∴DM=OC+OD=6，
∴顶点M坐标为（2，6）．
设抛物线解析式为：y=a（x﹣2）2+6，
∵点C（0，4）在抛物线上，
∴4=4a+6，
解得a= 
．
∴抛物线的解析式为：y= （x﹣2）2+6= x2+2x+4．
（2）
解：如答图1，过点P作PE⊥x轴于点E．
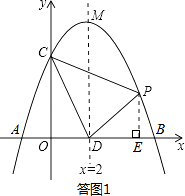
∵P（x，y），且点P在第一象限，
∴PE=y，OE=x，
∴DE=OE﹣OD=x﹣2．
S=S梯形PEOC﹣S△COD﹣S△PDE
= 
（4+y）x﹣ ×2×4﹣ （x﹣2）y
=y+2x﹣4．
将y= x2+2x+4代入上式得：S= x2+2x+4+2x﹣4= x2+4x．
在抛物线解析式y= x2+2x+4中，令y=0，即 x2+2x+4=0，解得x=2± 
．
设抛物线与x轴交于点A、B，则B（2+ ，0），
∴0＜x＜2+ ．
∴S关于x的函数关系式为：S= x2+4x（0＜x＜2+ ）．
（3）
解：存在．
若以O、P、E为顶点的三角形与△OPD全等，可能有以下情形：
（Ⅰ）OD=OP．
由图象可知，OP最小值为4，即OP≠OD，故此种情形不存在．
（Ⅱ）OD=OE．
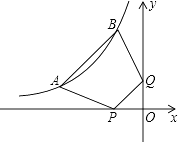
若点E在y轴正半轴上，如答图2所示：
此时△OPD≌△OPE，
∴∠OPD=∠OPE，即点P在第一象限的角平分线上，
所以P点的横纵坐标相等，即 x2+2x+4=x，解答x1=﹣2（舍去），x2=4．
所以P点坐标为：（4，4），
∴直线PE的解析式为：y= x+2；
若点E在y轴负半轴上，易知此种情形下，两个三角形不可能全等，故不存在．
（Ⅲ）OD=PE．
∵OD=2，
∴第一象限内对称轴右侧的点到y轴的距离均大于2，
则点P只能位于对称轴左侧或与顶点M重合．
若点P位于第一象限内抛物线对称轴的左侧，易知△OPE为钝角三角形，而△OPD为锐角三角形，则不可能全等；
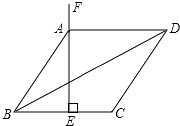
若点P与点M重合，如答图3所示，此时△OPD≌OPE，四边形PDOE为矩形，
∴直线PE的解析式为：y=6．
综上所述，存在以O、P、E为顶点的三角形与△OPD全等，直线PE的解析式为y=6，y= x+2．
【解析】（1）首先求出点M的坐标，然后利用顶点式和待定系数法求出抛物线的解析式；（2）如答图1所示，作辅助线构造梯形，利用S=S梯形PEOC﹣S△COD﹣S△PDE求出S关于x的表达式；求出抛物线与x轴正半轴的交点坐标，得到自变量的取值范围；（3）由于三角形的各边，只有OD=2是确定长度的，因此可以以OD为基准进行分类讨论：①OD=OP．因为第一象限内点P到原点的距离均大于4，因此OP≠OD，此种情形排除；②OD=OE．分析可知，只有如答图2所示的情形成立；③OD=PE．分析可知，只有如答图3所示的情形成立．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
