题目内容
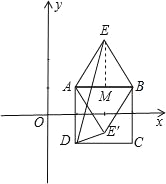
【题目】如图,点A(1,1),B(3,1),C(3,﹣1),D(1,﹣1)构成正方形ABCD,以AB为边做等边△ABE,则∠ADE和点E的坐标分别为( )

A. 15°和(2,1+![]() )
)
B. 75°和(2,![]() ﹣1)
﹣1)
C. 15°和(2,1+![]() )或75°和(2,
)或75°和(2,![]() ﹣1)
﹣1)
D. 15°和(2,1+![]() )或75°和(2,1﹣
)或75°和(2,1﹣![]() )
)
【答案】D
【解析】
分为两种情况:①当△ABE在正方形ABCD外时,过E作EM⊥AB于M,根据
等边三角形性质求出AM、AE,根据勾股定理求出EM,即可得出E的坐标,求出∠EAD,
根据三角形的内角和定理和等腰三角形性质即可求出∠ADE;②当等边△ABE在正方形
ABCD内时,同法求出此时E的坐标,求出∠DAE,根据三角形的内角和定理和等腰三角
形性质即可求出∠ADE.
分为两种情况:①△ABE在正方形ABCD外时,如图,过E作EM⊥AB于M,
∵等边三角形ABE,
∴AE=AB=3﹣1=2,
∴AM=1,
由勾股定理得:AE2=AM2+EM2,
∴22=12+EM2,
∴![]()
∵A(1,1),
∴E的坐标是![]()
∵等边△ABE和正方形ABCD,
∴∠DAB=90°,∠EAB=60°,AD=AE,
∴![]()
②同理当△ABE在正方形ABCD内时,同法求出E的坐标是![]()
∵∠DAE=90°﹣60°=30°,
AD=AE,
∴![]()
∴∠ADE和点E的坐标分别为15°,![]() 或75°,
或75°,![]()
故选:D.

练习册系列答案
相关题目