题目内容
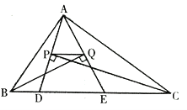
【题目】如图,△ABC的周长为30cm,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=11cm,则DE的长为____cm.
【答案】8
【解析】
证明△BQA≌△BQE,得到BA=BE,根据三角形的周长公式出去BE+CD,求出DE,根据三角形中位线定理计算即可.
解:∵BQ平分∠ABC,BQ⊥AE,
在△BQA和△BQE中,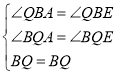 ,
,
∴△BQA≌△BQE,
∴BA=BE,
∴△BAE是等腰三角形,
同理△CAD是等腰三角形,
∴点Q是AE中点,点P是AD中点(三线合一),
∴PQ是△ADE的中位线,
∵BE+CD=AB+AC=30-BC=30-11=19,
∴DE=BE+CD-BC=8,
故答案为:8.

练习册系列答案
相关题目







