题目内容
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是 ![]() 的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
的中点,则下列结论:①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )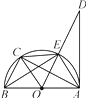
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】由C为 ![]() 的中点,利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE,故A正确;
的中点,利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE,故A正确;
由C为 ![]() 的中点,即
的中点,即 ![]() ,利用等弧对等弦,得到BC=EC,故B正确;
,利用等弧对等弦,得到BC=EC,故B正确;
由AD为圆的切线,得到AD⊥OA,进而确定出一对角互余,再由直角三角形ABE中两锐角互余,利用同角的余角相等,得到∠DAE=∠ABE,故C正确;
AC不一定垂直于OE,故D错误.
故答案为:D
利用垂径定理的逆定理得出OC⊥BE,由AB为圆的直径,利用直径所对的圆周角为直角得到AE⊥BE,即可确定出OC∥AE;利用等弧对等弦,得到BC=EC;利用同角的余角相等,得到∠DAE=∠ABE.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】如图,在△ABC 中,AB=AD,CB=CE.
(1)当∠ABC=90°时(如图①),∠EBD= °;
(2)当∠ABC=n°(n≠90)时(如图②),求∠EBD 的度数(用含 n 的式子表示).

【题目】某移动通信公司推出了如下两种移动电话计费方式,
月使用费/元 | 主叫限定时间/分钟 | 主叫超时费(元/分钟) | |
方式一 | 30 | 600 | 0.20 |
方式二 | 50 | 600 | 0.25 |
说明:月使用费固定收取,主叫不超过限定时间不再收费,超过部分加收超时费.例如,方式一每月固定交费30元,当主叫计时不超过300分钟不再额外收费,超过300分钟时,超过部分每分钟加收0.20元(不足1分钟按1分钟计算)
(1)请根据题意完成如表的填空;
月主叫时间500分钟 | 月主叫时间800分钟 | |
方式一收费/元 |
| 130 |
方式二收费/元 | 50 |
|
(2)设某月主叫时间为t(分钟),方式一、方式二两种计费方式的费用分别为y1(元),y2(元),分别写出两种计费方式中主叫时间t(分钟)与费用为y1(元),y2(元)的函数关系式;
(3)请计算说明选择哪种计费方式更省钱.