题目内容
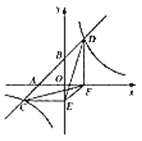
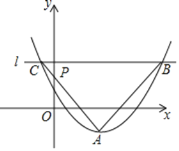
【题目】如图,在平面直角坐标系中,抛物线y=![]() -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
-1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=______.
【答案】3
【解析】
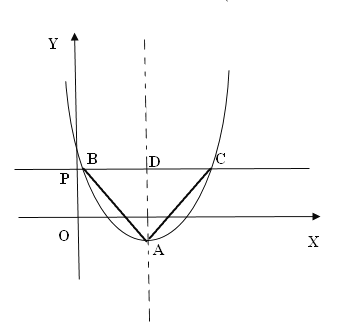
设直线l与对称轴的交点为点D,则根据等腰直角三角形的性质可得BD=AD,根据韦达定理可表示出x1+x2与x1x2,进而表示出BC的长度和BD的长度,根据BD=AD可列出方程求出m的值.
设直线l与对称轴的交点为点D,则根据等腰直角三角形的性质可得BD=AD,抛物线的顶点坐标为A(3,-1),
由题意得直线l的表达式为直线y=m,
当y=m时,可得方程![]()
原方程整理可得,![]()
由一元二次方程根与系数的关系可得x1+x2=6,x1x2=![]() ,
,
(x1-x2)2=(x1+x2)2-4 x1x2=36-20+16m=16+16m
∵直线l与抛物线交于点B和点C,
故m>-1,
∵BC2=16+16m,AD=m+1,BD=![]() =AD,
=AD,
∴BC=2AD,BC2=4AD2,
16+16m =4(m+1)2
整理得,m2-2m-3=0
解得m=3或m=-1(舍去)
即m=3.
故答案为3.

 阅读快车系列答案
阅读快车系列答案【题目】张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
步行数(步) | 10672 | 4927 | 5543 | 6648 | ||
步行距离(公里) | 6.8 | 3.1 | 3.5 | 4.6 | ||
卡路里消耗(千卡) | 157 | 73 | 82 | 107 | ||
燃烧脂肪(克) | 20 | 10 | 12 | 16 |
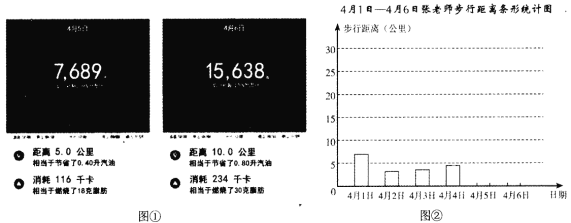
(1).请你将手环记录的4
(2).请你将条形统计图(如图②)补充完整.
(3).张老师这6天平均每天约步行____公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为_____公里(精确到0.1公里).