Question

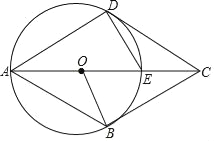
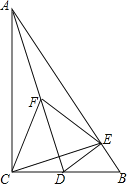
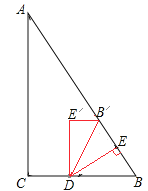
【题目】如图，在Rt△ABC中，∠ACB=90°，∠B=60°，D为BC上一点，过点D作DE⊥AB于E．

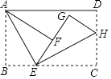
（1）连接AD，取AD中点F，连接CF，CE，FE，判断△CEF的形状并说明理由

（2）若BD=CD，将△BED绕着点D逆时针旋转n°（0＜n＜180），当点B落在Rt△ABC的边上时，求出n的值．

Answer 1

【答案】（1）△CEF是等边三角形．（2）n=60°或135°

【解析】

（1）根据直角三角形斜边的中线等于斜边的一半证得FC=FE即可，再证明∠CFE=60°，从而进行判断；

（2）根据∠B=60°，∠DEB=90°，可知BD=DE，又BD=CD，则DC=DE，将△BED绕着点D逆时针旋转n°（0＜n＜180），当点B落在Rt△ABC的边上时，∠CDE等于旋转角，∠CDE=180°-∠BDE=180°-30°=150°．

（1）∵∠ACB=90°，F是AD中点，

∴FC=AD，

∵DE⊥AB，F是AD中点，

∴EF=AD，

∴FC=FE，

∴△CEF是等腰三角形；

又EF=AF，CF=AF，故∠CFE=2∠CAB=60°

从而可知：△CEF是等边三角形．

（2）n=60°或135°

理由：①将△BED绕着点D逆时针旋转n°（0＜n＜180），当点B落在Rt△ABC的边AC上时，此时记为B'点，如图，

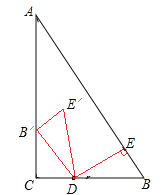
△B'CD为直角三角形，

又∵BD=CD，

故∠B'DC=45°；从而旋转角∠BDB'=180°-∠B'DC=180°-45°=135°

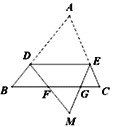
②当B'在边AB上时，有DB=DB'，又∠B=60°，故可知△DBB'为等边三角形，所以∠BDB'=60°，即n=60°.

如图，