题目内容
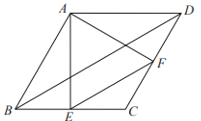
【题目】（发现）如图，点E，F分别在正方形ABCD的边BC，CD上，连接EF．因为AB=AD，所以把ΔABE绕A逆时针旋转90°至ΔADG，可使AB与AD重合．因为∠CDA=∠B=90°，所以∠FDG=180°，所以F、D、G共线．
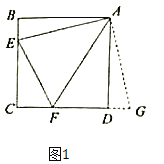
如果__________（填一个条件），可得ΔAEF≌ΔAGF．经过进一步研究我们可以发现：当BE，EF，FD满足__________时，∠EAF=45°．
（应用）
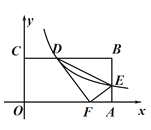
如图，在矩形ABCD中，AB=6，AD=m，点E在边BC上，且BE=2．
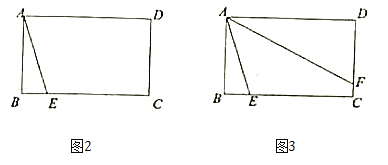
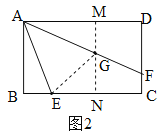
（1）若m=8，点F在边DC上，且∠EAF=45°（如图），求DF的长；
（2）若点F在边DC上，且∠EAF=45°，求m的取值范围．
【答案】发现：
（或
）（答案不唯一），
；应用：（1）
；（2）
【解析】
[发现]由旋转的性质及全等三角形的判定与性质即可得出结论；
[应用]（1）作正方形ABNM，MN与AF相交于点G，连接EG．设MG=x，则NG=6-x，由[发现]可得：BE+MG=EG，即2+x=EG．在Rt△ENG中，由勾股定理可得x的值，即MG的长，由相似三角形的性质得到AM：AD=MG：DF，即可得出结论；
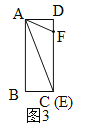
（2）当C和E重合时，如图3，m=AD=BC=2最小；
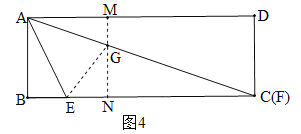
当C和F重合时，如图4，m=AD最大．类似（1）可得m的值．
[发现]∠EAF=∠GAF（或EF=FG）如图1所示：
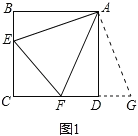
∵AB=AD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC=∠B=90°，∴∠FDG=180°，点F、D、G共线，∴∠DAG=∠BAE，AE=AG．
若添加条件为：∠EAF=∠GAF．
∵AE=AG，∠EAF=∠GAF，AF=AF，∴ΔAEF≌ΔAGF．
若添加条件为：EF=FG．
∵AE=AG，EF=FG，AF=AF，∴ΔAEF≌ΔAGF．
当BE+FD=EF时，∠EAF=45°．证明如下：
由旋转的性质可知：∠EAG=90°，△ABE≌△ADG，∴AE=AG，∠BAE=∠DAG，BE=DG．
∵BE+FD=EF，∴DG+FD=EF，∴FG=EF．
∵AE=AG，AF=AF，∴ΔAEF≌ΔAGF，∴∠EAF=∠FAG=45°．
[应用]（1）作正方形ABNM，MN与AF相交于点G，连接EG．设MG=x，则NG=6-x．
∵BE=2，∴EN=6-2=4．由[发现]可得：BE+MG=EG，∴2+x=EG．在Rt△ENG中，∵EN2+NG2=EG2，∴
，解得：x=3，∴MG=3．
∵MN∥DC，∴△AMG∽△ADF，∴AM：AD=MG：DF，∴6：8=3：DF，解得：DF=4．
（2）当C和E重合时，如图3，m=AD=BC=2最小；
当C和F重合时，如图4，m=AD最大．类似（1）可得：MG=3．
∵MN∥DC，∴△AMG∽△ADC，∴AM：MG=AD：DC，∴6：3=m：6，解得：m=12．
综上所述：2≤m≤12．
