题目内容
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,分别过
两点,分别过![]() 、
、![]() 两点作
两点作![]() 轴和
轴和![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() 、
、![]() ,连接
,连接![]() 、
、![]() .下列四个结论:①
.下列四个结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论是__________.(把你认为正确结论的序号都填上)
.其中正确的结论是__________.(把你认为正确结论的序号都填上)
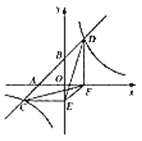
【答案】①②③④
【解析】
设D(x,![]() ),得出F(x,0),根据三角形的面积公式求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据相似三角形的判定判断②即可;证出平行四边形BDFE和平行四边形ACEF,可推出AC=BD,判断③即可;由一次函数解析式求得点A、B的坐标,结合锐角三角函数的定义判断④即可.
),得出F(x,0),根据三角形的面积公式求出△DEF的面积,同法求出△CEF的面积,即可判断①;根据相似三角形的判定判断②即可;证出平行四边形BDFE和平行四边形ACEF,可推出AC=BD,判断③即可;由一次函数解析式求得点A、B的坐标,结合锐角三角函数的定义判断④即可.
①设D(x,![]() ),则F(x,0),
),则F(x,0),
由图象可知x>0,k>0,
∴△DEF的面积是:![]() ×
×![]() ×x=
×x=![]() k,
k,
设C(a,![]() ),则E(0,
),则E(0,![]() ),
),
由图象可知:a>0,![]() <0,
<0,
△CEF的面积是:![]() ×|a|×|
×|a|×|![]() |=
|=![]() |k|,
|k|,
∴△CEF的面积=△DEF的面积,
故①正确;
②△CEF和△DEF以EF为底,则两三角形EF边上的高相等,
∴EF∥CD,
∴FE∥AB,
∴△AOB∽△FOE,
故②正确;
③∵BD∥EF,DF∥BE,
∴四边形BDFE是平行四边形,
∴BD=EF,
同理EF=AC,
∴AC=BD,
故③正确;
④由一次函数y=ax+b的图象与x轴,y轴交于A,B两点,
易得A(-![]() ,0),B(0,b),
,0),B(0,b),
则OA=![]() ,OB=b,
,OB=b,
∴tan∠BAO=![]() =a,
=a,
故④正确.
正确的有4个:①②③④.
故答案为:①②③④.

【题目】观察下表三行数的规律,回答下列问题:
第 | 第 | 第 | 第 | 第 | 第 | ... | |
第 |
|
|
|
|
|
| ... |
第 |
|
|
|
|
|
| ... |
第 |
|
|
|
|
|
| ... |
(1)第![]() 行的第四列数
行的第四列数![]() ______________,第
______________,第![]() 行的第六列数
行的第六列数![]() ______________;
______________;
(2)若第![]() 行的某一列的数为
行的某一列的数为![]() ,则第
,则第![]() 的式子表示);
的式子表示);
(3)已知第![]() 列的三个数的和为
列的三个数的和为![]() ,试求
,试求![]() 的值.
的值.