题目内容
【题目】如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG>60°.现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
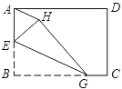
A. 5B. 3C. 2D. 1
【答案】B
【解析】
连接BH,根据折叠的性质得到∠1=∠2,EB=EH,BH⊥EG,则∠EBH=∠EHB,又点E是AB的中点,得EH=EB=EA,于是判断△AHB为直角三角形,且∠3=∠4,根据等角的余角相等得到∠1=∠3,因此有∠1=∠2=∠3=∠4.
解:连接BH,如图,
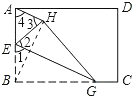
∵沿直线EG将纸片折叠,使点B落在纸片上的点H处,
∴∠1=∠2,EB=EH,BH⊥EG,
而∠1>60°,
∴∠1≠∠AEH,
∵EB=EH,
∴∠EBH=∠EHB,
又∵点E是AB的中点,
∴EH=EB=EA,
∴EH=![]() AB,
AB,
∴△AHB为直角三角形,∠AHB=90°,∠3=∠4,
∴∠1=∠3,
∴∠1=∠2=∠3=∠4.
则与∠BEG相等的角有3个.
故选:B.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目