题目内容
【题目】解不等式组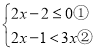
请结合题意填空,完成本题的解答
(1)解不等式①,得___________;
(2)解不等式②,得___________;
(3)把不等式①和②的解集在数轴上表示出来:
(4)原不等式组的解集为_______________.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)图见解析;(4)
;(3)图见解析;(4)![]() .
.
【解析】
(1)按照移项、系数化为1的步骤解不等式①即可;
(2)按照移项、合并同类项、系数化为1的步骤解不等式②即可;
(3)根据数轴的定义,将不等式①和②的解集在数轴上表示出来即可;
(4)找出(3)中的公共部分即可.
(1)移项,得![]()
系数化为1,得![]()
故答案为:![]() ;
;
(2)移项,得![]()
合并同类项,得![]()
系数化为1,得![]()
故答案为:![]() ;
;
(3)把不等式①和②的解集在数轴上表示出来如下所示:
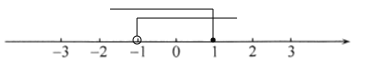
(4)找出(3)中的公共部分得:原不等式组的解集为![]()
故答案为:![]() .
.

练习册系列答案
相关题目
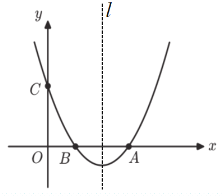
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3