Question

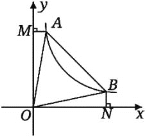
【题目】如图，在平面直角坐标系中，抛物线与x轴交于点A，B（1，0），与轴交于点C（0，3），对称轴为直线．

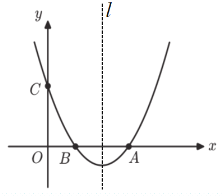
(1)求抛物线的解析式及点A的坐标；

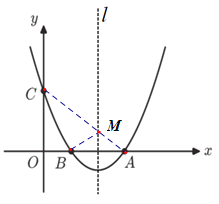
(2)在对称轴上是否存在一点M，使得△BCM周长最小？若存在，求出△BCM周长；若不存在，请说明理由；

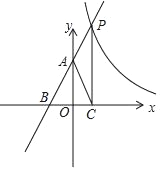
(3)若点P是抛物线上一动点，从点C沿抛物线向点A运动，过点P作PD//轴，交AC于点D，当△ADP是直角三角形时，求点P的坐标．

Answer 1

【答案】（1）y=x2﹣4x+3；（2）存在，；（3）P（1,0）或（2，-1）

【解析】

（1）用待定系数法求解即可；

（2）连接AC交直线于点M，连接BM．由轴对称的性质可知此时BM+MC=AM+MC=AC，即△ABM周长最短；

（3）分当∠APD=90°时和当∠PAD=90°时两种情况求解即可．

解：（1）将B(1，0)，C(0，3)代入中，得

，解得，

∴抛物线解析式为y=x2﹣4x+3；

（2）存在．

连接AC交直线于点M，连接BM．

∵点A，B关于直线对称，

∴BM=CM，

∴BM+MC=AM+MC=AC，

∴此时△ABM周长最短．

∵，

∴△ABM的周长最小为AC+BC=；

（3）由题得，A(3，0)，B(1，0)，C(0，3)，

∴OA=OC ，∴∠CAO=45°，

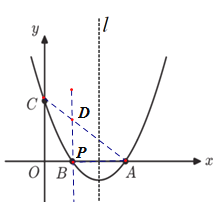
当∠APD=90°时，∵PD//y轴，AB⊥y轴，

∴PD⊥AB，∴点P与点B重合，

∴P点坐标为（1，0）；

当∠PAD=90°时，则∠PAB=∠DAB=45°，

∵AB⊥PD，∴，

设直线AC的解析式为y=kx+b，

把A(3，0)， C(0，3)代入得

，

解得

，

∴直线AC的解析式为y=-x+3，

设点D(m，-m+3)，点P(m，m2﹣4m+3)，

∴，解得（舍去），

∴P点坐标为(2，-1)，

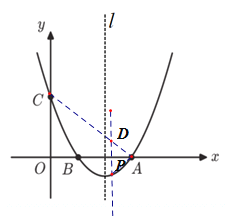
综上所述，P(1，0)或(2，-1)．