Question

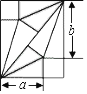
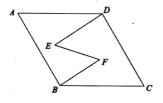
【题目】如图，已知在菱形中，， 则菱形的边长等于____________

Answer 1

【答案】

【解析】

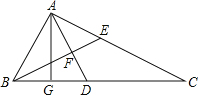
作BG⊥EF，连接BD，与EF相交于点H，由三角函数求出BG和GF的长度，然后得到EG的长度，由DE∥BF，则△DEH∽△BFH，则，设GH=x，则EH=2+x，FH=3-x，代入求出GH，再由勾股定理求出BH，得到BD的长度，即可得到菱形的边长．

解：作BG⊥EF，连接BD，与EF相交于点H，如图：

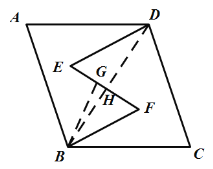
∵DE∥BF，

∴∠F=∠E，

∴sin∠F=sin∠E=，

∵BG⊥EF，

∴，

∵BF=EF=5，

∴BG=4，

∴FG=，

∴EG=5；

∵DE∥BF，

∴△DEH∽△BFH，

∴，

设GH=x，则EH=2+x，FH=3-x，

∴，

解得：，

∴；

在Rt△BGH中，由勾股定理，得

，

∴；

∵∠A=60°，AB=AD，

∴△ABD是等边三角形，

∴；

故答案为：．