题目内容
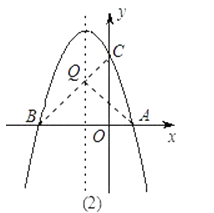
【题目】如图，抛物线y=﹣x2+bx+c与x轴交于A（1，0），B（﹣3，0）两点．
（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
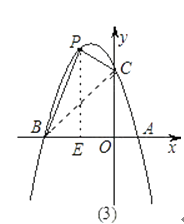
（3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？若存在，求出点P的坐标及△PBC的面积最大值；若没有，请说明理由．
【答案】
（1）
解：将A（1，0），B（﹣3，0）代y=﹣x2+bx+c中得
∴ 
∴抛物线解析式为：y=﹣x2﹣2x+3
（2）
解：存在
理由如下：由题知A、B两点关于抛物线的对称轴x=﹣1对称
∴直线BC与x=﹣1的交点即为Q点，此时△AQC周长最小
∵y=﹣x2﹣2x+3
∴C的坐标为：（0，3）
直线BC解析式为：y=x+3
Q点坐标即为 
解得 
∴Q（﹣1，2）
（3）
解：存在．
理由如下：设P点（x，﹣x2﹣2x+3）（﹣3＜x＜0）
∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣ 
若S四边形BPCO有最大值，则S△BPC就最大，
∴S四边形BPCO=S△BPE+S直角梯形PEOC
= 
BEPE+ OE（PE+OC）
= （x+3）（﹣x2﹣2x+3）+ （﹣x）（﹣x2﹣2x+3+3）
= 
当x=﹣ 
时，S四边形BPCO最大值= 
∴S△BPC最大= 
当x=﹣ 时，﹣x2﹣2x+3= 
∴点P坐标为（﹣ ， ）
【解析】（1）根据题意可知，将点A、B代入函数解析式，列得方程组即可求得b、c的值，求得函数解析式；（2）根据题意可知，边AC的长是定值，要想△QAC的周长最小，即是AQ+CQ最小，所以此题的关键是确定点Q的位置，找到点A的对称点B，求得直线BC的解析式，求得与对称轴的交点即是所求（3）存在，设得点P的坐标，将△BCP的面积表示成二次函数，根据二次函数最值的方法即可求得点P的坐标．
