Question

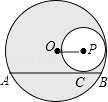
【题目】已知抛物线C：y2=4x的焦点为F，准线为l．⊙F与C交于A，B两点，与x轴的负半轴交于点P． （Ⅰ）若⊙F被l所截得的弦长为 ，求|AB|；
（Ⅱ）判断直线PA与C的交点个数，并说明理由．

Answer 1

【答案】解：（Ⅰ）抛物线C：y2=4x的焦点为F（1，0）， ∵⊙F被l所截得的弦长为 ，
∴圆的半径为 =3，
∴⊙F的方程为（x﹣1）2+y2=9，
与y2=4x联立可得A（2，2 ），B（2，﹣2 ），∴|AB|=4 ；
（Ⅱ）（x﹣1）2+y2=9，令y=0，可得P（4，0），
∵A（2，2 ），∴直线PA与C的交点个数为2．
【解析】（Ⅰ）若⊙F被l所截得的弦长为 ，求出圆的半径，得到圆的方程，即可求|AB|；（Ⅱ）求出P的坐标，即可判断直线PA与C的交点个数，