题目内容
【题目】△ABC中,D为线段BC的中点,AB=2AC=2,tan∠CAD=sin∠BAC,则BC= .
【答案】![]()
【解析】解:如图, 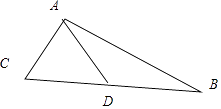
设∠CAD=α,∠BAD=β,则∠CAB=α+β.
则有 ![]() ,
, ![]() ,且sin∠ADC=sin∠ADB,AB=2AC,可得sinα=2sinβ.
,且sin∠ADC=sin∠ADB,AB=2AC,可得sinα=2sinβ.
由题意知tan∠CAD=sin∠CAB,即tanα=sin(α+β).
切化弦可得 ![]() ,
,
故sinα=sin(α+β)cosα,从而可得2sinβ=sin(α+β)cosα,
利用角的变形可得2sin[(α+β)﹣α]=sin(α+β)cosα,
展开得sin(α+β)cosα=2cos(α+β)sinα,两边同除以cosα(cosα≠0)
可得sin(α+β)=2cos(α+β)tanα,又因为tanα=sin(α+β),
化简得2cos(α+β)=1,故 ![]() .
.
所以BC2=AB2+AC2﹣2ABACcos(α+β)=3,故 ![]() .
.
所以答案是: ![]()

练习册系列答案
相关题目



