ЬтФПФкШн
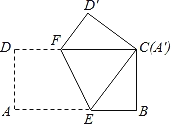
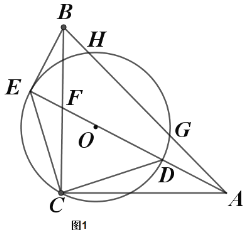
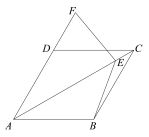
ЁОЬтФПЁПдкСтаЮABCDжаЃЌЁЯBAD=![]() ЃЌEЮЊЖдНЧЯпACЩЯЕФвЛЕуЃЈВЛгыAЃЌCжиКЯЃЉЃЌНЋЩфЯпEBШЦЕуEЫГЪБеыа§зЊ
ЃЌEЮЊЖдНЧЯпACЩЯЕФвЛЕуЃЈВЛгыAЃЌCжиКЯЃЉЃЌНЋЩфЯпEBШЦЕуEЫГЪБеыа§зЊ![]() НЧжЎКѓЃЌЫљЕУЩфЯпгыжБЯпADНЛгкFЕуЃЎЪдЬНОПЯпЖЮEBгыEFЕФЪ§СПЙиЯЕЃЎ
НЧжЎКѓЃЌЫљЕУЩфЯпгыжБЯпADНЛгкFЕуЃЎЪдЬНОПЯпЖЮEBгыEFЕФЪ§СПЙиЯЕЃЎ
аЁгюЗЂЯжЕуEЕФЮЛжУЃЌ![]() КЭ
КЭ![]() ЕФДѓаЁЖМВЛШЗЖЈЃЌгкЪЧЫћДгЬиЪтЧщПіПЊЪМНјааЬНОПЃЎ
ЕФДѓаЁЖМВЛШЗЖЈЃЌгкЪЧЫћДгЬиЪтЧщПіПЊЪМНјааЬНОПЃЎ
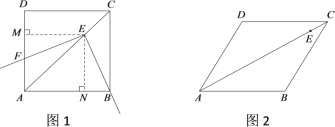
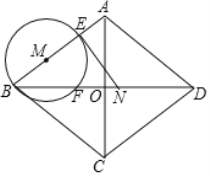
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() =
=![]() =90ЁуЪБЃЌСтаЮABCDЪЧе§ЗНаЮЃЎаЁгюЗЂЯжЃЌдке§ЗНаЮжаЃЌACЦНЗжЁЯBADЃЌзїEMЁЭADгкMЃЌENЁЭABгкNЃЎгЩНЧЦНЗжЯпЕФаджЪПЩжЊEM=ENЃЌНјЖјПЩЕУ
=90ЁуЪБЃЌСтаЮABCDЪЧе§ЗНаЮЃЎаЁгюЗЂЯжЃЌдке§ЗНаЮжаЃЌACЦНЗжЁЯBADЃЌзїEMЁЭADгкMЃЌENЁЭABгкNЃЎгЩНЧЦНЗжЯпЕФаджЪПЩжЊEM=ENЃЌНјЖјПЩЕУ![]() ЃЌВЂгЩШЋЕШШ§НЧаЮЕФаджЪЕУЕНEBгыEFЕФЪ§СПЙиЯЕЮЊ ЃЎ
ЃЌВЂгЩШЋЕШШ§НЧаЮЕФаджЪЕУЕНEBгыEFЕФЪ§СПЙиЯЕЮЊ ЃЎ
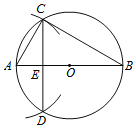
ЃЈ2ЃЉШчЭМ2ЃЌЕБ![]() =60ЁуЃЌ
=60ЁуЃЌ![]() =120ЁуЪБЃЌ
=120ЁуЪБЃЌ
ЂйвРЬтвтВЙШЋЭМаЮЃЛ
ЂкЧыАяаЁгюМЬајЬНОПЃЈ1ЃЉЕФНсТлЪЧЗёГЩСЂЃЎШєГЩСЂЃЌЧыИјГіжЄУїЃЛШєВЛГЩСЂЃЌЧыОйГіЗДР§ЫЕУїЃЛ
ЃЈ3ЃЉаЁгюдкРћгУЬиЪтЭМаЮЕУЕНСЫвЛаЉНсТлжЎКѓЃЌдкДЫЛљДЁЩЯЖдвЛАуЕФЭМаЮНјааСЫЬНОПЃЌЩшЁЯABE=![]() ЃЌШєа§зЊКѓЫљЕУЕФЯпЖЮEFгыEBЕФЪ§СПЙиЯЕТњзуЃЈ1ЃЉжаЕФНсТлЃЌЧыжБНгаДГіНЧ
ЃЌШєа§зЊКѓЫљЕУЕФЯпЖЮEFгыEBЕФЪ§СПЙиЯЕТњзуЃЈ1ЃЉжаЕФНсТлЃЌЧыжБНгаДГіНЧ![]() ,
,![]() ЃЌ
ЃЌ![]() ТњзуЕФЙиЯЕЃК ЃЎ
ТњзуЕФЙиЯЕЃК ЃЎ
ЁОД№АИЁПЃЈ1ЃЉEB=EFЃЛЃЈ2ЃЉЂйВЙШЋЭМаЮМћНтЮіЃЛЂкНсТлвРШЛГЩСЂEB=EFЃЎжЄУїМћНтЮіЃЛ ЃЈ3ЃЉ![]() ЁуЃЈЕБBЕФЖдГЦЕуВЛЮЊDЪБЃЉЛђ
ЁуЃЈЕБBЕФЖдГЦЕуВЛЮЊDЪБЃЉЛђ![]() ЁуЃЈЕБBЕФЖдГЦЕуЮЊDЪБЃЉ
ЁуЃЈЕБBЕФЖдГЦЕуЮЊDЪБЃЉ
ЁОНтЮіЁП
(1)ЯШжЄУїANEMЪЧе§ЗНаЮЃЌдйжЄУї![]() ЃЌМДПЩжЄЕУНсЙћЃЛ
ЃЌМДПЩжЄЕУНсЙћЃЛ
(2)ЂйВЙШЋЭМаЮШчЭМЫљЪОЃЛ
ЂкжЄЗЈ1ЃЌгУНЧЦНЗжЯпаджЪЕУГіEM=EN,дйжЄУїГі![]() ЃЌМДПЩЃЛ
ЃЌМДПЩЃЛ
жЄЗЈ2ЃЌРћгУСтаЮЕФаджЪжБНгГіЁїADEЁеЁїABEЃЎМДПЩЕУГіНсТлЃЛ
(3)жБНгЕУГіНсТлЁЃ
ЃЈ1ЃЉEB=EFЃЛ
ЃЈ2ЃЉЂйВЙШЋЭМаЮШчЭМЫљЪОЃЛ
ЂкНсТлвРШЛГЩСЂEB=EFЃЎ
жЄЗЈ1ЃКЙ§ЕуEзїEMЁЭAFгкMЃЌENЁЭABгкNЃЎ
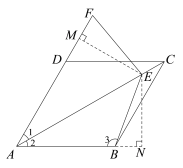
ЁпЫФБпаЮABCDЮЊСтаЮЃЌ
Ёр![]() ЃЎ
ЃЎ
ЁпEMЁЭAFЃЌENЁЭABЃЎ
Ёр![]() ЁуЃЌEM=ENЃЎ
ЁуЃЌEM=ENЃЎ
Ёп![]() ЁуЃЌ
ЁуЃЌ![]() ЁуЃЌ
ЁуЃЌ
Ёр![]() Ёу
Ёу![]() ЁуЃЎ
ЁуЃЎ
Ёп![]() ЁуЃЌ
ЁуЃЌ
Ёр![]() ЃЎ
ЃЎ
дкЁїEFMгыЁїEBNжаЃЌ
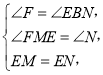
ЁрЁїEFM ЁеЁїEBNЃЎ
ЁрEF=EBЃЎ
жЄЗЈ2ЃКСЌНгED
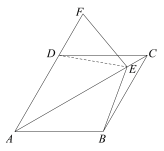
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрAD=ABЃЌЁЯDAC=ЁЯBAEЃЎ
гжЁпAE=AE,
ЁрЁїADEЁеЁїABEЃЎ
ЁрED=EBЃЌЁЯADE=ЁЯABEЃЎ
гжЁпЁЯDAB=60ЁуЃЌЁЯBEF=120ЁуЃЎ
ЁрЁЯF+ЁЯABE=180ЁуЃЎ
гжЁпЁЯADE+ЁЯFDE=180ЁуЃЌ
ЁрЁЯF=ЁЯFDEЃЎ
ЁрEF=EDЃЎ
ЁрEF=EBЃЎ
ЃЈ3ЃЉ![]() ЁуЃЈЕБBЕФЖдГЦЕуВЛЮЊDЪБЃЉЛђ
ЁуЃЈЕБBЕФЖдГЦЕуВЛЮЊDЪБЃЉЛђ![]() ЁуЃЈЕБBЕФЖдГЦЕуЮЊDЪБЃЉ.
ЁуЃЈЕБBЕФЖдГЦЕуЮЊDЪБЃЉ.

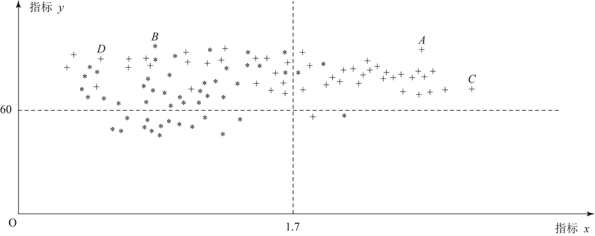
ЁОЬтФПЁПдкаХЯЂПьЫйЗЂеЙЕФЩчЛсЃЌЁАаХЯЂЯћЗбЁБвбГЩЮЊШЫУЧЩњЛюЕФживЊзщГЩВПЗжЃЌФГИпаЃзщжЏПЮЭтаЁзщдкЮвЪаЕФвЛИіЩчЧјЫцЛњГщШЁВПЗжМвЭЅЃЌЕїВщУПдТгУгкаХЯЂЯћЗбЕФН№ЖюЃЌИљОнЪ§ОнећРэГЩШчЯТВЛЭъећЭГМЦБэКЭЭГМЦЭМЃЈШчЭМЃЉЃЎвбжЊ![]() ЃЌ
ЃЌ![]() СНзщЛЇЪ§ЦЕЪ§вЫЗНЭМЕФИпЖШБШЮЊ1ЃК5ЃЎ
СНзщЛЇЪ§ЦЕЪ§вЫЗНЭМЕФИпЖШБШЮЊ1ЃК5ЃЎ
дТаХЯЂЯћЗбЖюЗжзщЭГМЦБэ
зщБ№ | ЯћЗбЖю/дЊ |
|
|
|
|
|
|
|
|
|
|
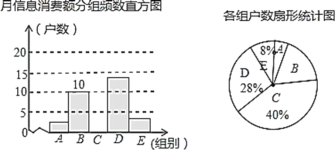
ЧыНсКЯЭМБэжаЯрЙиЪ§ОнНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉетДЮНгЪмЕїВщЕФга_________ЛЇЃЛ
ЃЈ2ЧыФуВЙШЋЦЕЪ§жБЗНЭМЃЛ
ЃЈ3ЃЉвдИїзщзщжажЕДњБэБОзщЕФдТаХЯЂЯћЗбЖюЕФЦНОљЪ§ЃЌМЦЫуПЮЭтаЁзщГщШЁМвЭЅЕФдТаХЯЂЯћЗбЖюЕФЦНОљЪ§ЃЛ
ЃЈ4ЃЉШєИУЩчЧјга2000ЛЇзЁЛЇЃЌЧыЙРМЦдТаХЯЂЯћЗбЖюВЛЩйгк200дЊЕФЛЇЪ§ЪЧЖрЩйЃП