题目内容
【题目】在平面直角坐标系
中，反比例函数
的图象与直线
交于点
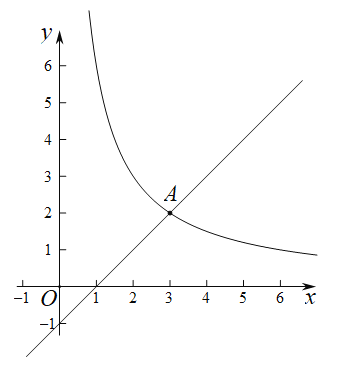
（1）求k的值；
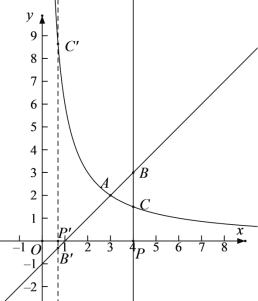
（2）已知点
，过点P作垂直于x轴的直线，交直线于点B，交函数于点C．
①当
时，判断线段
与
的数量关系，并说明理由；
②若
，结合图象，直接写出n的取值范围．
【答案】（1）
；（2）①
，
；理由见解析；②
或
．
【解析】
（1）把点A的坐标代入一次函数解析式即可求出m的值，再把点A的坐标代入反比例函数解析式即可求出k的值；
（2）①把x=4分别代入一次函数和反比例函数解析式求出点B和点C的坐标，即可判断出PC与PB的数量关系；
②结合图象及①中结论可得当n≥4或点B在x轴或x轴下方时PC≤PB，即可确定出对应的n的取值范围．
（1）把
代入
得
，
，
又
图象过点
，
解得；
（2）①
，
当
时，
，
，
，，
所以；
②根据图象可得：或．
练习册系列答案
相关题目
【题目】五名学生投篮球，每人投10次，统计他们每人投中的次数．得到五个数据，并对数据进行整理和分析给出如下信息：
平均数 | 中位数 | 众数 |
m | 6 | 7 |
则下列选项正确的是（ ）
A.可能会有学生投中了8次
B.五个数据之和的最大值可能为30
C.五个数据之和的最小值可能为20
D.平均数m一定满足
