题目内容
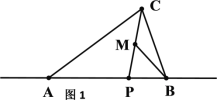
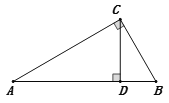
【题目】如图，Rt△ABC中，∠ACB＝90°，∠A＝30°，CD⊥AB于D，△BCD的周长为（6＋2
）cm，则△ABC的周长为（ ）cm．
A.（9＋2）B.（12＋）C.（12＋4）D.（18＋2）
【答案】C
【解析】
由已知Rt△ABC中，∠ACB=90°，∠A=30°，CD⊥AB于点D，可得∠BCD=∠A=30°，根据含30度角的直角三角形的性质，可得：BC=
AB，BD=BC，CD=AC，求出△BCD与△ABC的周长之比之后即可求△ABC的周长；
解：
已知Rt△ABC中，∠ACB=90°，∠A=30°，
∵CD⊥AB，
∴∠BCD=∠A=30°，
∴BC=AB，BD=BC，CD=AC，
∴BC+BD+CD=(AB+BC+AC)，
则
=，
∴△BCD与△ABC的周长之比为：，
∵△BCD的周长为（6＋2
），
∴△ABC的周长为2×（6＋2）=12＋4；
故选C.
练习册系列答案
名校课堂系列答案
相关题目
