题目内容
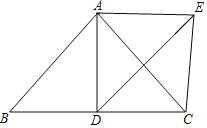
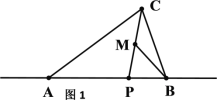
【题目】如图1,在△ABC中,点P为边AB所在直线上一点,连结CP,M为线段CP的中点,若满足∠ACP=∠MBA,则称点P为△ABC的“好点”.
(1)如图2,当∠ABC=90°时,命题“线段AB上不存在“好点”为 (填“真”或“假”)命题,并说明理由;
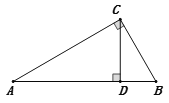
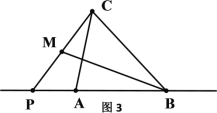
(2)如图3,P是△ABC的BA延长线的一个 “好点”,若PC=4,PB=5,求AP的值;
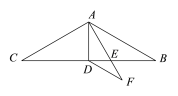
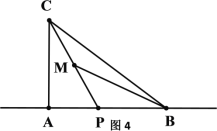
(3)如图4,在Rt△ABC中,∠CAB=90°,点P是△ABC的“好点”,若AC=4,AB=5,求AP的值.

【答案】(1)真;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先根据直角三角形斜边的中线等于斜边的一半可知MP=MB,从而∠MPB=∠MBP,然后根据三角形外角的性质说明即可;
(2)先证明△PAC∽△PMB,然后根据相似三角形的性质求解即可;
(3)分三种情况求解:P为线段AB上的“好点”, P为线段AB延长线上的“好点”, P为线段BA延长线上的“好点”.
(1)真 .
理由如下:如图,当∠ABC=90°时,M为PC中点,BM=PM,
则∠MPB=∠MBP>∠ACP,
所以在线段AB上不存在“好点”;
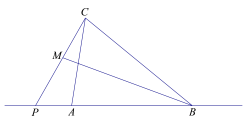
(2)∵P为BA延长线上一个“好点”;
∴∠ACP=∠MBP;
∴△PAC∽△PMB;
∴![]() 即
即![]() ;
;
∵M为PC中点,
∴MP=2;
∴![]() ;
;
∴![]() .
.
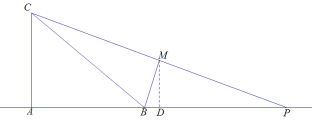
(3)第一种情况,P为线段AB上的“好点”,则∠ACP=∠MBA,找AP中点D,连结MD;
∵M为CP中点;
∴MD为△CPA中位线;
∴MD=2,MD//CA;
∴∠DMP=∠ACP=∠MBA;
∴△DMP∽△DBM;
∴DM2=DP·DB即4= DP·(5![]() DP);
DP);
解得DP=1,DP=4(不在AB边上,舍去;)
∴AP=2
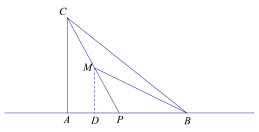
第二种情况(1),P为线段AB延长线上的“好点”,则∠ACP=∠MBA,找AP中点D,此时,D在线段AB上,如图,连结MD;
∵M为CP中点;
∴MD为△CPA中位线;
∴MD=2,MD//CA;
∴∠DMP=∠ACP=∠MBA;
∴△DMP∽△DBM
∴DM2=DP·DB即4= DP·(5![]() DA)= DP·(5
DA)= DP·(5![]() DP);
DP);
解得DP=1(不在AB延长线上,舍去),DP=4
∴AP=8;
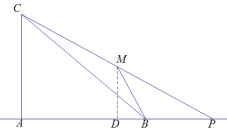
第二种情况(2),P为线段AB延长线上的“好点”,找AP中点D,此时,D
此时,∠MBA>∠MDB>∠DMP=∠ACP,则这种情况不存在,舍去;

第三种情况,P为线段BA延长线上的“好点”,则∠ACP=∠MBA,
∴△PAC∽△PMB;
∴![]()
∴BM垂直平分PC则BC=BP=![]() ;
;
∴![]()
∴综上所述,![]() 或
或![]() 或
或![]() ;
;

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案