题目内容
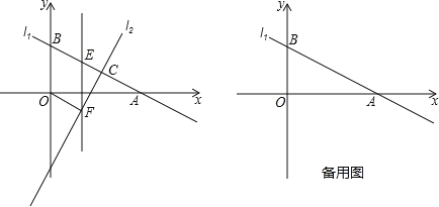
【题目】如图，直线l1：y=-0.5x+b分别与x轴、y轴交于A．B两点，与直线l2：y=kx-6交于点C（4，2）．
（1）点A坐标为（______，______），B为（______，______）；
（2）在线段BC上有一点E，过点E作y轴的平行线交直线l2于点F，设点E的横坐标为m，当m为何值时，四边形OBEF是平行四边形．
【答案】（1）8，0，0， 4 ；（2）当m为2.4时，四边形OBEF是平行四边形．
【解析】
（1）由点C的坐标，利用待定系数法可求出直线l1的解析式，再利用一次函数图象上点的坐标特征可求出点A，B的坐标；
（2）由点C的坐标，利用待定系数法可求出直线l2的解析式，利用一次函数图象上点的坐标特征可得出点E，F的坐标，进而可得出EF的长，再利用平行四边形的性质即可得出关于m的一元一次方程，解之即可得出结论．
解：（1）将C（4，2）代入y=-0.5x+b，得：
-2+b=2，解得：b=4，
∴直线l1的解析式为y=-0.5x+4．
当x=0时，y=-0.5x+4=4，
∴点B的坐标为（0，4）；
当y=0时，-0.5x+4=0，
解得：x=8，
∴点A的坐标为（8，0）．
故答案为：（8，0）；（0，4）．
（2）将C（4，2）代入y=kx-6，得，
，解得：
，
∴直线
的解析式为y=2x-6．
∵点E的横坐标为
，则其纵坐标为
，点F的横坐标为m，其纵坐标为
，
∵
，
若四边形OBEF是平行四边形，
则
，
∴
解得：
，
∴当m为2.4时，四边形OBEF是平行四边形．
【题目】随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为2000元、1700元的A、B两种型号的净水器，下表是近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 18000元 |
第二周 | 4台 | 10台 | 31000元 |
（1）分别求A、B两种型号的净水器的销售单价；
（2）若该电器公司准备用不多于54000元的金额采购这两种型号的净水器共30台，求A种型号的净水器最多能采购多少台？
