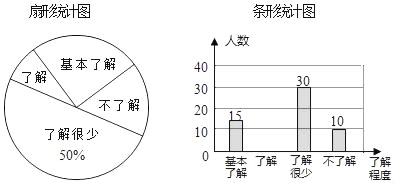
题目内容
【题目】（1）在等腰三角形ABC，∠A＝130°，求∠B的度数
（2）在等腰三角形ABC中，∠A＝40°，求∠B的度数．
（3）根据（1）（2）问后发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A＝x°，当∠B有三个不同的度数时,请你探索x的取值范围，并用含x的式子表示∠B的度数．
【答案】（1）∠B=25°；（2）∠B＝70°或100°或40°；（3）当x≠60时，∠B有三个不同的度数，∠B的度数为（
）°或（180﹣2x）°或x°．
【解析】
（1）根据三角形内角和定理，因为∠A＝130°＞90°，得到∠B＝∠C＝25°；
（2）根据三角形内角和定理，因为∠A＝40°＜90°，所以有∠A＝∠B或∠A＝∠C或∠B＝∠C，分别求出∠B的度数即可；
（3）分两种情况：①当90≤x＜180时，∠B的度数只有一个，不符合条件；②当0＜x＜90时，结合三角形内角和定理先求出三种情况时∠B的度数，再根据∠B的三个度数不同求解即可．
解：（1）根据三角形内角和定理，
∵∠A＝130°＞90°，
∴∠B＝∠C＝（180°-130°）÷2=25°；
（2）若∠A为顶角，则∠B＝（180°﹣∠A）÷2＝70°；
若∠A为底角，∠B为顶角，则∠B＝180°﹣2×40°＝100°；
若∠A为底角，∠B为底角，则∠B＝∠A=40°；
故∠B＝70°或100°或40°；
（3）分两种情况：
①当90≤x＜180时，∠A只能为顶角，
∴∠B的度数只有一个，∠B＝（）°，不符合条件；
②当0＜x＜90时，
若∠A为顶角，则∠B＝（）°；
若∠A为底角，∠B为顶角，则∠B＝（180﹣2x）°；
若∠A为底角，∠B为底角，则∠B＝x°．
∵∠B有三个不同的同的度数，
∴≠180﹣2x，180﹣2x≠x或≠x，
解得x≠60，
即当x≠60时，∠B有三个不同的度数，∠B的度数为（）°或（180﹣2x）°或x°．
【题目】某天，一蔬菜经营户用 1200 元钱按批发价从蔬菜批发市场买了西红柿和豆角共 400 kg，然后在市场上按零售价出售，西红柿和豆角当天的批发价和零售价如表所示：
品名 | 西红柿 | 豆角 |
批发价（单位：元/kg） | 2.4 | 3.2 |
零售价（单位：元/kg） | 3.8 | 5.2 |
（1）该经营户所批发的西红柿和豆角的质量分别为多少 kg？
（2）如果西红柿和豆角全部以零售价售出，他当天卖出这些西红柿和豆角赚了多少钱？
