Question

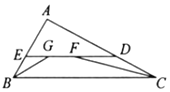
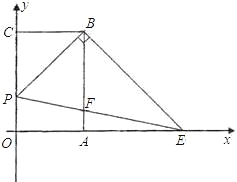
【题目】如图，已知矩形OABC，以点O为坐标原点建立平面直角坐标系，其中A（2，0），C（0，3），点P以每秒1个单位的速度从点C出发在射线CO上运动，连接BP，作BE⊥PB交x轴于点E，连接PE交AB于点F，设运动时间为t秒．

（1）当t=2时，求点E的坐标；

（2）若AB平分∠EBP时，求t的值.

（3）在运动的过程中，是否存在以P、O、E为顶点的三角形与△ABE相似．若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）E（5，0）；（2）∴t=2；（3）存在；（0，）或（0，）．

【解析】

（1）本题需先求出AB=AE，再求出DE=5，即可求出点E的坐标．
（2）本题需先求出CP=CB=2，即可求出t的值．
（3）本题需先证出△BCP∽△BAE，求出AE=t，再分两种情形分别求解即可解决问题；

解：（1）当t=2时，PC=2，

∵BC=2，

∴PC=BC，

∴∠PBC=45°，

∴∠BAE=90°，

∴∠AEB=45°，

∴AB=AE=3，

∴OE=5,

∴点E的坐标是（5，0）；

（2）当AB平分∠EBP时，

∠PBF=45°，

则∠CBP=∠CPB=45°，

∴CP=CB=2,

∴t=2；

（3）存在，

∵∠ABE+∠ABP=90°，

∠PBC+∠ABP=90°，

∴∠ABE=∠PBC，

∵∠BAE=∠BCP=90°，

∴△BCP∽△BAE，

∴ ，

∴ ，

∴ t，

∵若△POE∽△EAB，

∴ ,

∴，

∴t1= ，t2=（舍去），

∴P的坐标为（0， ）；

当点P在y轴的负半轴上时，若△POE∽△EAB，则有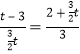，无解，

若△POE∽△BAE，则有：，

解得t=3+ 或3﹣（舍弃）

∴P的坐标为（0，）或（0，）．